DART

Back in 2005, researchers at Microsoft came up with a concolic testing tool called DART(Directed Automated Random Testing). The tool can be used in the unit testing phase, as well as can be applied to large programs.

We present a new tool, named DART, for automatically testing software that combines three main techniques: (1) automated extraction of the interface of a program with its external environment using static source-code parsing; (2) automatic generation of a test driver for this interface that performs random testing to simulate the most general environment the program can operate in; and (3) dynamic analysis of how the program behaves under random testing and automatic generation of new test inputs to direct systematically the execution along alternative program paths.

Breaking down the three techniques mentioned:

For given functions f and h,

int f (int x) { 
	return 2 * x;
}

int h (int x, int y) {
	if (x != y)
		if (f(x) == x + 10) ➊
			abort(); /* error */
	return 0;
}
  1. Automated interface extraction:
    • The static source code is parsed to find the program’s interfaces.
      • Inputs - arguments given to the main function, variables with environment dependent values and external function calls, any database fetch for data.
      • Outputs - any data sent to the console.
    • In the example, static parsing would show that the function takes two integer arguments as input, namely, x and y.
  2. Automatic generation of a test driver for random testing through the interface:
    • Once the interfaces have been determined, a test driver can be generated to simulate the testing of the program in the most general environment that the program is meant to operate in.
    • The framework attempts the exploration of all execution paths by randomly initializing all local and external variables, and simulates all the external functions.
    • In the example, the variables will initially be assigned random values, say x = 5. On reaching ➊, a condition is encountered and branches are discovered. The path constraint is evaluated to be (2 * x) == (x + 10).
  3. Dynamic test generation to direct execution along alternative program paths:
    • Execution is started with a random input, and then the inputs for the next execution are calculated by a solving the symbolic constraints encountered in the current execution.
    • This allows DART to perform a directed search, as the new input vector shall “direct” the execution of the program through a new path to cover newer regions of the binary.
    • This process is looped till full coverage of the binary is achieved or a bug is encountered.
    • In the example, a constraint solver will solve the condition encountered to find the values, x = 10 here, will move the program forward towards the unexplored branches, and provide that as the input vector in the next execution to explore that particular branch.

Therefore, DART eliminates the requirement of writing a test driver and a corresponding harness for testing of the given program. It detects the output during all test cases and checks for standard errors such as violations and crashes.

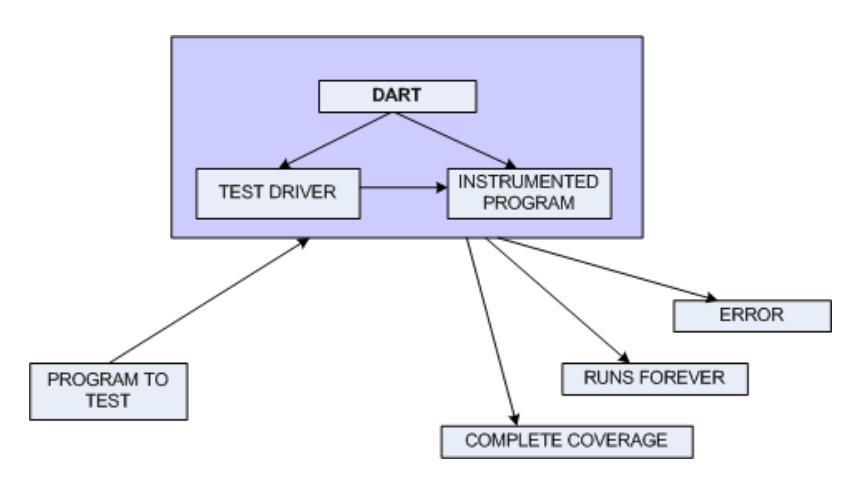DART overview.

Execution Model

DART executes a program P both concretely and symbolically, in parallel. The concrete execution is given concrete values as input, decided by the symbolic execution, which allows it to collect various path constraints that are solved to generate inputs for the next test case. 

A transition system is required to maintain this side-by-side execution, which is basically a state machine. This represents(tracks) values of all variables and program counter, and a transition denotes the execution of a program statement(machine level instructions) that results in the change of state. Therefore, each execution would result in a path through this transition system. These semantics require assistance of RAM to keep track of such program statements.

This parallel execution can be summarized as:

The program P defines a sequence of input addresses for the input parameters. A randomly initialized vector associates a value to each input parameter, thus defining the initial value for the set of these input addresses, defined as state M.

Let C be the set of conditional statements encountered in P.

Let A be the set of assignment statements encountered in P.

Then, execution of a program statement can be denoted as follows:

M’ := M + [ m → v ]

where,

       M is the mapping of a memory address space beginning from m to n-bit words (n can be taken as 32).

       + denotes updation.

       → denotes assignment.

       m is a memory address, which may or may not be holding a symbolic variable.

       M’ is therefore same as M, except that m is updated to the value v.

⇨ M’ = v

Thus, M and M’ are the states (also called context), and the updated value v is the solution for the constraint and will be used as input in the next execution.

This program execution E is a finite sequence which goes on until an abort is encountered (such as a program crash) or a halt is encountered (such as program termination). This execution process can be denoted as follows:

E := (A ⋃ C) * (abort | halt)

This E(P) can be viewed as a tree, known as execution tree, where different paths branching from the current state are children of the current node, with leaf nodes being the abort and halt states. Each execution sequence is therefore a path in this tree.

Symbolic Evaluation Model

DART maintains a symbolic memory map S that maps memory address to symbolic expressions. During the execution process, DART constantly evaluates the path constraints encountered to generate new input vector for the subsequent executions. Only linear path constraints are supported. Any non-linear constraint is ignored and concrete values are used instead of symbolic values.

During the initiation of execution of P, S records the mapping of random values to input parameters. The following algorithms takes an expression e in a context M with already available expression set S and is evaluated as follows:

evaluate_symbolic (e, M, S):
	
	// Switch case to match expression.
	match e:
		
		// Case is only a symbolic variable.
		case m:
			
			// Directly assign it to the symbolic expression set.
			if m ∈ domain S then return S(m)
			
			// Return the updated memory.
			else return M(m)
		
		// Case is any arithmetic operation (multiplication in this case).
		case ∗(e', e''):
			
			// Evaluate the symbolic expressions individually first.
			let f’ = evaluate_symbolic(e', M, S);
			let f” = evaluate_symbolic(e'', M, S);
			
			// If none of the evaluated results are constants, then the constraint becomes non-linear.
			if not one of f' or f'' is a constant c then
				
				// Since DART doesn't work with non-linear constraints, unset linearity flag.
				➋ all_linear = 0
				// Simply performs concrete evaluation and update the memory, it doesn't store the constraint.
				return evaluate_concrete(e, M)
			
			// No expression to evaluate so simply performs concrete evaluation.
			if both f' and f'' are constants then
				return evaluate_concrete(e, M)
			
			// If either one is a constant, it'll evaluate the expression and return.
			if f' is a constant c then
				return ∗(f' , c)
			else return ∗(c, f\'\')
		
		// Case is pointer dereference.
		case ∗e':
			
			// Symbolically evaluate the expression at the address first.
			let f’= evaluate_symbolic(e' ,M, S);
			
			// If the result is constant
			if f' is a constant c then
			
				// The expression it is pointing to belongs to the set of expressions, return itself.
				if ∗c ∈ domain S then return S ∗ c
				
				// Return pointer to the memory location.
				else return M(∗c)
			
			// If it cannot determine either of the aforementioned cases, set all memory locations are not definitely known.
			else ➌ all_locs_definite = 0
			
				// Simply performs concrete evaluation and update the memory.
				return evaluate concrete(e, M)

It’s possible for DART to not know all the memory locations definitely (➌) because it doesn’t always evaluate all the symbolic expressions (➋).

Test Driver

The primary task of the test driver is to combine random testing with directed search. Any exception encountered during this process indicates a bug.

Two completeness flags work in conjunction to indicate cases when symbolic execution is not performed:

  1. all_linear: set to 0 when symbolic expression becomes non-linear (➋).
  2. all_locs_definite: set to 0 when value of a symbolic variable is unknown (➌).
run DART () =

	// Initialise all flags to 1.
	all linear, all locs definite, forcing ok = 1, 1, 1
	
	// Random testing loop.
	repeat
	
		// Initialise stack to empty, input vector to empty and set directed search to true.
		stack = <>; I = [] ; directed = 1
		
		// Perform directed search.
		while (directed) do
		
			// Run instrumented program.
			try (directed, stack, I) =
				instrumented program(stack, I)
				
			// Any exception encoutered implies a bug has been found.
			catch any exception →
				if (forcing ok)
					print “Bug found”
					exit()
				
				// Forces exit in the next iteration if a bug has been found.
				else forcing ok = 1
		
	// Exit testing if any completeness flags is set to 0.
	until all_linear ∧ all_locs_definite

Once the directed search ends, and if the completeness flags still hold true(both set to 1), then the outer loop exits. DART has then said to have explored all feasible program paths. However, any one of the completeness flags set to 0 during the testing process indicates a bad situation. And if any one of them get’s turned off during execution, the random testing process will continue till manually stopped.

Each run of the instrumented program is executed with the results of the conditional statements in the previous execution (except the first run, it is with random values). And for each conditional statement, we note:

  1. branch value: set to 1 when the then branch is taken, 0 otherwise.
  2. done value: set to 0 only when one branch of conditional has executed in the prior runs, 1 otherwise.

This information associated with each conditional statement of the last execution path is stored in the stack.

Therefore, for i ∈ 0 ≤ i ≤ |stack|, stack[i] = (stack[i].branch, stack[i].done) is the record corresponding to the (i + 1_) conditional statement.

The program is instrumented as follows:

instrumented program(stack, I) =

	// Random initialization of uninitialized input parameters in M0.
	for each input x with I[x] undefined do
			I[x] = random()
	
	//Initialize memory M from M0 and I.

	// Set up symbolic memory and prepare execution.
	S = [m → m | m ∈ M0].
	
	// Initial program counter in P.
	l = l0
		
	// Number of conditionals executed.
	k = 0 
	
	// Now invoke P intertwined with symbolic calculations.
	s = statement_at(l, M)
	
	// Loop till an abort or a halt is encountered.
	while (s ∈ { / abort, halt}) do
	
		// Match the case of a program statement.
		match (s)
		
			// Assignment statement.
			case (m ← e):
			
				// Memory location for m is updated.
				S = S + [m → evaluate_symbolic(e, M, S)]
				
				// Evaluates expression e concretely.
				v = evaluate_concrete(e, M)
				
				// Update the memory location as well.
				M = M + [m → v]
				
				// Increment the program counter after executing current statement.
				l = l0 + 1
			
			// Conditional statement.
			case (if (e) then goto l'):
			
				// Evalaute e concretely.
				b = evaluate_concrete(e, M)
				
				// Evaluate e symbolically.
				c = evaluate_symbolic(e, M, S)
				
				
				// Already have a path constraint.
				if b then
				
					// c has been added to the path constraint via bitwise AND.
					path_constraint = path_constraint ^ <c>
					
					// Push the current state to stack.
					stack = compare_and_update_stack(1, k,stack)
					
					// Jump to label.
					l = l'
				
				else
					// c's negation has been added to the path constraint via bitwise AND.
					path constraint = path_constraint ^ <-(c)>
					
					// Push the current state to stack.
					stack = compare_and_update_stack(0, k,stack)
					
					// Increment the program counter after executing current statement.
					l = l0 + 1
					
				// Keep track of conditionals.
				k = k + 1
				
		s = statement_at(l, M)
	
	// If an abort is encountered in the execution, raise exception.
	if (s == abort) then
		raise an exception
		
	// If a halt is encountered, it'll solve path constraints.
	else
		return solve_path_constraint(k, path_constraint, stack)

compare_and_update_stack(branch, k, stack) is just a generic stack operation function used to check whether the current execution path matches the one predicted at the end of the previous execution and represented in stack passed between runs. If the prediction fails, forcing_ok flag is set to 0 and the instrumentation is restarted with a fresh random input vector.

statement_at(l, M) fetches the next instruction to be executed in the context of M.

Any third party constraint solver can be employed for the task. An abstraction of the working of a suitable constraint solver is as follows:

solve_path_constraint(ktry, path_constraint, stack) =

	// Take latest path constraint from the stack.
	let j be the smallest number such that
		for all h with −1 ≤ j<h<ktry, stack[h].done = 1
		
	// If none is found, directed search is finished.
	if j = −1 then
		return (0, , )
	else
	
		// Negate the path constraint found at the top of the stack.
		path_constraint[j] = neg(path_constraint[j])
		
		// Add it to the branch.
		stack[j].branch= ¬stack[j].branch
		
		// Call that branch to explore it.
		if (path constraint[0,... ,j] has a solution I) then
			return (1,stack[0..j], I
		else
			solve_path_constraint(j, path_constraint, stack)

 

SAGE

Following the success of DART, a new framework known as SAGE(Scalable, Automated, Guided Execution) was born in 2008 that employs DART in the background, to perform fuzzing on large applications (mainly file-reading applications) by using symbolic execution of the target programs at the x86 binary level. It’s an extremely versatile tool since it is machine-code based, hence can run binaries programmed using various programming languages.

We present an alternative whitebox fuzz testing approach inspired by recent advances in symbolic execution and dynamic test generation. Our approach records an actual run of the program under test on a well-formed input, symbolically evaluates the recorded trace, and gathers constraints on inputs capturing how the program uses these. The collected constraints are then negated one by one and solved with a constraint solver, producing new inputs that exercise different control paths in the program. This process is repeated with the help of a code-coverage maximizing heuristic designed to find defects as fast as possible.

A Generation Search Algorithm can described as follows:

  • Systematically explores execution of large applications with large input and deep paths.
  • Employs heuristics to maximize code coverage quickly, which would lead to finding bugs faster.
  • Resilient to divergences. Whenever it occurs, search is able to recover and continue.

SAGE basically performs a generational search repeating the following tasks:

  1. Tester: harness functionality executing the program with random inputs.
  2. Tracer: records logs of execution of the target binary.
  3. CoverageCollector:  computes the statistics on basic blocks which were executed during the run by going through the recorded execution.
  4. SymbolicExecution: replays the recorded execution to collect input related constraints and generate new inputs using a constraint solver.

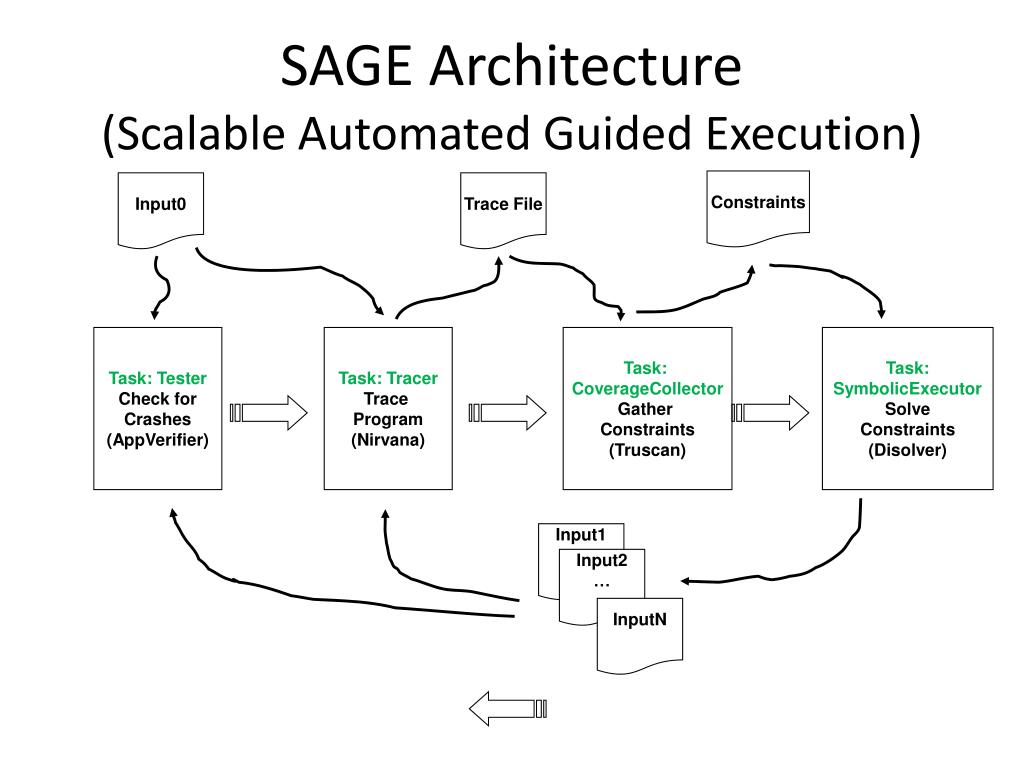Tasks running in order.

These tasks are optimized to handle large execution traces with features like constraint caching, common subexpression elimination and prevention of endless loop expansions.

Citation: DART, DART: Directed Automated Random Testing, From Blackbox Fuzzing to Whitebox Fuzzing towards Verification, Automated Whitebox Fuzz Testing, Automated Whitebox Fuzz Testing PPT.