Refer to this repository for solution scripts and the IPython Notebook pertaining to the explanations here.

Challenge 33: Implement Diffie-Hellman

Link

For one of the most important algorithms in cryptography this exercise couldn’t be a whole lot easier.
Set a variable “p” to 37 and “g” to 5. This algorithm is so easy I’m not even going to explain it. Just do what I do.
Generate “a”, a random number mod 37. Now generate “A”, which is “g” raised to the “a” power mode 37 — A = (g**a) % p.
Do the same for “b” and “B”.
“A” and “B” are public keys. Generate a session key with them; set “s” to “B” raised to the “a” power mod 37 — s = (B**a) % p.
Do the same with A**b, check that you come up with the same “s”.
To turn “s” into a key, you can just hash it to create 128 bits of key material (or SHA256 it to create a key for encrypting and a key for a MAC).
Ok, that was fun, now repeat the exercise with bignums like in the real world. Here are parameters NIST likes:
p:
ffffffffffffffffc90fdaa22168c234c4c6628b80dc1cd129024
e088a67cc74020bbea63b139b22514a08798e3404ddef9519b3cd
3a431b302b0a6df25f14374fe1356d6d51c245e485b576625e7ec
6f44c42e9a637ed6b0bff5cb6f406b7edee386bfb5a899fa5ae9f
24117c4b1fe649286651ece45b3dc2007cb8a163bf0598da48361
c55d39a69163fa8fd24cf5f83655d23dca3ad961c62f356208552
bb9ed529077096966d670c354e4abc9804f1746c08ca237327fff
fffffffffffff
g: 2
This is very easy to do in Python or Ruby or other high-level languages that auto-promote fixnums to bignums, but it isn’t “hard” anywhere.
Note that you’ll need to write your own modexp (this is blackboard math, don’t freak out), because you’ll blow out your bignum library raising “a” to the 1024-bit-numberth power. You can find modexp routines on Rosetta Code for most languages.

# Imports
import os
import struct
import random

# Given
p = 37
g = 5

The math involved in DHKE is very straightforward. Wikipedia provides a simple explanation:

The protocol uses the multiplicative group of integers modulo p, where p is prime, and g is a primitive root modulo p. These two values are chosen in this way to ensure that the resulting shared secret can take on any value from 1 to p–1. Here is an example of the protocol, with non-secret values in blue, and secret values in red.

  1. Alice and Bob publicly agree to use a modulus p = 23 and base g = 5 (which is a primitive root modulo 23).
  2. Alice chooses a secret integer a = 4, then sends Bob A = g_a_ mod p
    • A = 54 mod 23 = 4
  3. Bob chooses a secret integer b = 3, then sends Alice B = g_b_ mod p
    • B = 53 mod 23 = 10
  4. Alice computes s = B_a_ mod p
    • s = 104 mod 23 = 18
  5. Bob computes s = A_b_ mod p
    • s = 43 mod 23 = 18
  6. Alice and Bob now share a secret (the number 18).

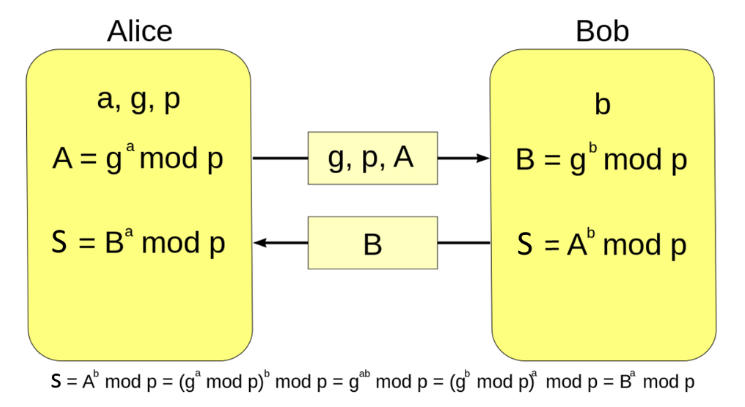The concept is that after all the computation involved, the two parties will end up with a common secret value.

class DiffieHellman():
    """
    Implements the Diffie-Helman key exchange. Each class is a party, which has his secret key (usually
    referred to as lowercase a or b) shares the public key (usually referred to as uppercase A or B) and can
    compute the shared secret key between itself and another party, given their public key, assuming that
    they are agreeing on the same p and g.
    """

    DEFAULT_G = 2
    DEFAULT_P = int('ffffffffffffffffc90fdaa22168c234c4c6628b80dc1cd129024e088a67cc74020bbea63b139b225'
                    '14a08798e3404ddef9519b3cd3a431b302b0a6df25f14374fe1356d6d51c245e485b576625e7ec6f4'
                    '4c42e9a637ed6b0bff5cb6f406b7edee386bfb5a899fa5ae9f24117c4b1fe649286651ece45b3dc20'
                    '07cb8a163bf0598da48361c55d39a69163fa8fd24cf5f83655d23dca3ad961c62f356208552bb9ed5'
                    '29077096966d670c354e4abc9804f1746c08ca237327ffffffffffffffff', 16)

    def __init__(self: object, g=DEFAULT_G, p=DEFAULT_P):
        self.g = g
        self.p = p
        self._secret_key = random.randint(0, p - 1)
        self.shared_key = None

    def gen_public_key(self: object) -> int:
        return pow(self.g, self._secret_key, self.p)

    def gen_shared_secret_key(self: object, other_party_public_key: int) -> int:
        if self.shared_key is None:
            self.shared_key = pow(other_party_public_key, self._secret_key, self.p)
        return self.shared_key

Create public and private keys for Alice and Bob.

# Alice
a = random.randint(0, 100)
A = (g**a) % p

# Bob
b = random.randint(0, 100)
B = (g**b) % p

Verify that the final session key comes out to be the same at Alice and Bob’s end.

session_key_Alice = (B**a) % p
session_key_Bob = (A**b) % p

assert session_key_Alice == session_key_Bob

Verify that our DiffieHellman implementation works and two parties will agree on the same key.

client1 = DiffieHellman()
client2 = DiffieHellman()

assert client1.gen_shared_secret_key(client2.gen_public_key()) == client2.gen_shared_secret_key(client1.gen_public_key())

Completed
 

Challenge 34: Implement a MITM key-fixing attack on Diffie-Hellman with parameter injection

Link

Use the code you just worked out to build a protocol and an “echo” bot. You don’t actually have to do the network part of this if you don’t want; just simulate that. The protocol is:
A->B
Send “p”, “g”, “A”
B->A
Send “B”
A->B
Send AES-CBC(SHA1(s)[0:16], iv=random(16), msg) + iv
B->A
Send AES-CBC(SHA1(s)[0:16], iv=random(16), A’s msg) + iv
(In other words, derive an AES key from DH with SHA1, use it in both directions, and do CBC with random IVs appended or prepended to the message).
Now implement the following MITM attack:
A->M
Send “p”, “g”, “A”
M->B
Send “p”, “g”, “p”
B->M
Send “B” M->A
Send “p” A->M
Send AES-CBC(SHA1(s)[0:16], iv=random(16), msg) + iv
M->B
Relay that to B B->M
Send AES-CBC(SHA1(s)[0:16], iv=random(16), A’s msg) + iv
M->A
Relay that to A
M should be able to decrypt the messages. “A” and “B” in the protocol — the public keys, over the wire — have been swapped out with “p”. Do the DH math on this quickly to see what that does to the predictability of the key.
Decrypt the messages from M’s vantage point as they go by.
Note that you don’t actually have to inject bogus parameters to make this attack work; you could just generate Ma, MA, Mb, and MB as valid DH parameters to do a generic MITM attack. But do the parameter injection attack; it’s going to come up again.

# Imports
import os
import random
import hashlib
from Crypto.Cipher import AES

# Given
p = 37
g = 5

The idea here is that the client sends (p, g, A) to the server, and the server responds with B. If you recall, p and g are the public agreed-upon parameters for the group prime and generator. A is the Client’s piece of the secret key, and B is the Server’s piece.

If an attacker replaces A and B with p, then both Client and Server will compute the key to be pᵃ mod p  = pᵇ mod p = 0 = pᵃ mod p =pᵇ mod p = 0. 

0 is then hashed and used as the symmetric key for AES-encrypting messages, so the attacker can decrypt all the communications.

def parameter_injection_attack(alice: object, bob: object):
    block_size = AES.block_size
    # A -> M
    A = alice.gen_public_key()
    # M -> B
    A = alice.p
    # B -> M
    B = bob.gen_public_key()
    # M -> A
    B = bob.p
    
    # A -> M
    msg = b"Hello there!"
    s_a = hashlib.sha1(str(alice.gen_shared_secret_key(B)).encode()).digest()[:AES.block_size]
    iv = os.urandom(16)
    cipher_a = AES_CBC_encrypt(msg, iv, s_a) + iv
    
    # M -> B
    
    # B -> M
    s_b = hashlib.sha1(str(bob.gen_shared_secret_key(A)).encode()).digest()[:16]
    a_iv = cipher_a[-AES.block_size:]
    a_msg = AES_CBC_decrypt(cipher_a[:-AES.block_size], iv, s_b)
    print("A sent:", PKCS7_unpad(a_msg))
    iv = os.urandom(16)
    cipher_b = AES_CBC_encrypt(a_msg, iv, s_b) + iv
    
    # M -> A
    
    # Finding the key after replacing A and B with p is, in fact, very easy.
    # Instead of (B^a % p) or (A^b % p), the shared secret key of the exercise became (p^a % p)
    # and (p^b % p), both equal to zero!
    mitm_key = hashlib.sha1(b'0').digest()[:AES.block_size]
    
    mitm_iv_a = cipher_a[-block_size:]
    mitm_msg_a_read = AES_CBC_decrypt(cipher_a[:-block_size], mitm_iv_a, mitm_key)
    print("MITM MSG A:", PKCS7_unpad(mitm_msg_a_read))
    
    mitm_iv_b = cipher_b[-block_size:]
    mitm_msg_b_read = AES_CBC_decrypt(cipher_b[:-block_size], mitm_iv_b, mitm_key)
    print("MITM MSG B:", PKCS7_unpad(mitm_msg_b_read))

alice = DiffieHellman(g, p)
bob = DiffieHellman(g, p)

parameter_injection_attack(alice, bob)

A sent: b'T\x1ezoR\x17vx\xc3\x99\xc2\x8d\xc2\xa4{Ey$('
MITM MSG A: b'T\x1ezoR\x17vx\xc3\x99\xc2\x8d\xc2\xa4{Ey$('
MITM MSG B: b'T\x1ezoR\x17vx\xc3\x83\xc2\x99\xc3\x82\xc2\x8d\xc3\x82\xc2\xa4{Ey$('

Completed
 

Challenge 35: Implement DH with negotiated groups, and break with malicious “g” parameters

Link

A->B
Send “p”, “g”
B->A
Send ACK
A->B
Send “A”
B->A
Send “B”
A->B
Send AES-CBC(SHA1(s)[0:16], iv=random(16), msg) + iv
B->A Send AES-CBC(SHA1(s)[0:16], iv=random(16), A’s msg) + iv
Do the MITM attack again, but play with “g”. What happens with:
g = 1
g = p
g = p - 1
Write attacks for each.

# Imports
import os
import hashlib
from Crypto.Cipher import AES

The idea here is that:

  1. For g = 1, 
    • all powers of g are 1 as well, so the secret key is always 1.
  2. For g = p, 
    • as we saw in the previous challenge, powers are all divisible by p, so the key is always 0. 
  3. For g = p-1,
    • g = p−1 is raised to a power, all the terms with p will be 0 mod p, leaving either 1 or -1 = (p-1) mod p.
def malicious_g_attack():
    """
    Simulates the break of Diffie-Hellman with negotiated groups by using malicious 'g' parameters.
    """
    
    p = DiffieHellman.DEFAULT_P
    return_vals = []

    # This loops over the values proposed for "g" by the question.
    for g in [1, p, p - 1]:

        # Step 1: the MITM changes the default g sent by Alice to Bob with a forced value.
        alice = DiffieHellman()
        bob = DiffieHellman(g=g)

        # Step 2: Bob receives this forced g and sends an ACK to Alice.

        # Step 3: Alice computes A and sends it to the MITM (thinking of Bob).
        A = alice.gen_public_key()

        # Step 4: Bob computes B and sends it to the MITM (thinking of Alice).
        B = bob.gen_public_key()

        # Step 5: Alice sends her encrypted message to Bob (without knowledge of MITM).
        _msg = b"Hello, how are you?"
        _a_key = hashlib.sha1(str(alice.gen_shared_secret_key(B)).encode()).digest()[:16]
        _a_iv = os.urandom(AES.block_size)
        a_question = AES_CBC_encrypt(_msg, _a_iv, _a_key) + _a_iv

        # Step 6: Bob receives the message sent by Alice (without knowing of the attack)
        # However, this time Bob will not be able to decrypt it, because (if I understood the
        # challenge task correctly) Alice and Bob now use different values of g.

        # Step 7: the MITM decrypts the Alice's question.
        mitm_a_iv = a_question[-AES.block_size:]

        # When g is 1, the secret key is also 1.
        if g == 1:
            mitm_hacked_key = hashlib.sha1(b'1').digest()[:16]
            mitm_hacked_message = AES_CBC_decrypt(a_question[:-AES.block_size], mitm_a_iv, mitm_hacked_key)

        # When g is equal to p, it works the same as in the S5C34 attack (the secret key is 0).
        elif g == p:
            mitm_hacked_key = hashlib.sha1(b'0').digest()[:16]
            mitm_hacked_message = AES_CBC_decrypt(a_question[:-AES.block_size], mitm_a_iv, mitm_hacked_key)

        # When g is equal to p - 1, the secret key is (-1)^(ab), which is either (+1 % p) or (-1 % p).
        # We can try both and later check the padding to see which one is correct.
        else:

            for candidate in [str(1).encode(), str(p - 1).encode()]:
                mitm_hacked_key = hashlib.sha1(candidate).digest()[:16]
                mitm_hacked_message = AES_CBC_decrypt(a_question[:-AES.block_size], mitm_a_iv, mitm_hacked_key)
                if PKCS7_padded(mitm_hacked_message):
                    mitm_hacked_message = PKCS7_unpad(mitm_hacked_message)
                    break
        print(mitm_hacked_message)

malicious_g_attack()

b'Hello, how are you?\r\r\r\r\r\r\r\r\r\r\r\r\r'
b'Hello, how are you?\r\r\r\r\r\r\r\r\r\r\r\r\r'
b'Hello, how are you?'

Completed
 

Challenge 36: Implement Secure Remote Password (SRP)

Link

To understand SRP, look at how you generate an AES key from DH; now, just observe you can do the “opposite” operation an generate a numeric parameter from a hash. Then:
Replace A and B with C and S (client & server)
C & S
Agree on N=[NIST Prime], g=2, k=3, I (email), P (password)
S
Generate salt as random integer
Generate string xH=SHA256(salt|password)
Convert xH to integer x somehow (put 0x on hexdigest)
Generate v=g**x % N
Save everything but x, xH
C->S
Send I, A=g**a % N (a la Diffie Hellman)
S->C
Send salt, B=kv + g**b % N
S, C
Compute string uH = SHA256(A|B), u = integer of uH
C
Generate string xH=SHA256(salt|password)
Convert xH to integer x somehow (put 0x on hexdigest)
Generate S = (B - k * g**x)**(a + u * x) % N
Generate K = SHA256(S)
S
Generate S = (A * v**u) ** b % N
Generate K = SHA256(S)
C->S
Send HMAC-SHA256(K, salt)
S->C
Send “OK” if HMAC-SHA256(K, salt) validates
You’re going to want to do this at a REPL of some sort; it may take a couple tries.
It doesn’t matter how you go from integer to string or string to integer (where things are going in or out of SHA256) as long as you do it consistently. I tested by using the ASCII decimal representation of integers as input to SHA256, and by converting the hexdigest to an integer when processing its output.
This is basically Diffie Hellman with a tweak of mixing the password into the public keys. The server also takes an extra step to avoid storing an easily crackable password-equivalent.

# Imports
import os
import web
import json
import time
import random
import hashlib

# Client and server agree on these values beforehand

# Generated using "openssl dhparam -text 1024".
N = int("008c5f8a80af99a7db03599f8dae8fb2f75b52501ef54a827b8a1a586f14dfb20d6b5e2ff878b9ad6bca0bb9"
        "18d30431fca1770760aa48be455cf5b949f3b86aa85a2573769e6c598f8d902cc1a0971a92e55b6e04c4d07e"
        "01ac1fa9bdefd1f04f95f197b000486c43917568ff58fafbffe12bde0c7e8f019fa1cb2b8e1bcb1f33", 16)
g = 2
k = 3
I = "hextersik@hexterisk.com"
P = "hexterisk"

I used web.py to build the server.

urls = (
    '/hello', 'Hello',
    '/init', 'Initiate',
    '/verify', 'Verify'
)

app = web.application(urls, globals())

K = None
salt = str(random.randint(0, 2**32 - 1))
# since we can't save x, xH
v = pow(g, int(hashlib.sha256(salt.encode()+P.encode()).hexdigest(), 16), N)

class Hello:        
    
    def GET(self):
        params = web.input()
        name = params.name
        if not name:
            name = 'World'
            
        string = "Hello, " + name + "!"
        return {"name" : string}
    
class Verify:

    def GET(self):
        
        global K, salt
        
        params = web.input()
        hmac_received = params.hmac
        
        HMAC_obj = HMAC(K, hashlib.sha256)
        hmac = HMAC_obj.compute(salt.encode())
        
        if hmac == hmac_received:
            return "OK"

class Initiate:
    
    def GET(self):
        
        global K, salt
        
        params = web.input()
        I = params.I
        A = int(params.A)
        
        b = random.randint(0, N - 1)
        B = k*v + pow(g, b, N)
        
        uH = hashlib.sha256(str(A).encode()+str(B).encode()).hexdigest()
        u = int(uH, 16)
        S = pow(A * pow(v, u, N), b, N)
        K = hashlib.sha256(str(S).encode()).digest()
        
        return {"salt":salt, "B":B}

Test the web server.

response1 = app.request("/hello?name=")
print(response1.data)

response2 = app.request("/hello?name=hexterisk")
print(json.loads(response2.data.decode("utf-8").replace("'",'"')))

b"{'name': 'Hello, World!'}"
{'name': 'Hello, hexterisk!'}

SRP (Secure Remote Protocol) is an authentication method where the user/client need not share their password. Rather, the server stores a verifier:

v = gˣ , where x = H(salt || password).

After exchanging various parameters, both the client and the server generate a session key K. The server generates it with the verifier while the client generates it with the password. The server checks that the value of K should be same on both ends.

Refer Wikipedia for a complete explanation.

def implement_SRP() -> bool:
    """
    Implements SRP(Secure Remote Password).
    """
    
    a = random.randint(0, N - 1)
    A = pow(g, a, N)
    
    response = app.request("/init?I=" + I + "&A=" + str(A))
    response_dict = json.loads(response.data.decode("utf-8").replace("'",'"'))
    salt = response_dict["salt"]
    B = int(response_dict["B"])

    uH = hashlib.sha256(str(A).encode()+str(B).encode()).hexdigest()
    u = int(uH, 16)
    
    xH = hashlib.sha256(salt.encode()+P.encode()).hexdigest()
    x = int(xH, 16)
    
    S = pow((B - k * pow(g, x, N)), (a + u * x), N)
    K = hashlib.sha256(str(S).encode()).digest()

    HMAC_obj = HMAC(K, hashlib.sha256)
    hmac = HMAC_obj.compute(salt.encode())
    
    response = app.request("/verify?hmac=" + hmac)
    assert response.data.decode("utf-8") == "OK"
    print("> Verification successful.")
    return True

> Verification successful.

Completed
 

Challenge 37: Break SRP with a zero key

Link

Get your SRP working in an actual client-server setting. “Log in” with a valid password using the protocol.
Now log in without your password by having the client send 0 as its “A” value. What does this to the “S” value that both sides compute?
Now log in without your password by having the client send N, N*2, &c.

# Imports
import os
import web
import json
import time
import random
import hashlib

I used web.py to build the server.

NOTE: The attack is only possible if the server doesn’t check the value of client’s public key against zero.

urls = (
    '/hello', 'Hello',
    '/init', 'Initiate',
    '/verify', 'Verify'
)

app = web.application(urls, globals())

K = None
salt = str(random.randint(0, 2**32 - 1))
# since we can't save x, xH
v = pow(g, int(hashlib.sha256(salt.encode()+P.encode()).hexdigest(), 16), N)

class Hello:        
    
    def GET(self):
        params = web.input()
        name = params.name
        if not name:
            name = 'World'
            
        string = "Hello, " + name + "!"
        return {"name" : string}
    
class Verify:

    def GET(self):
        
        global K, salt
        
        params = web.input()
        hmac_received = params.hmac
        
        HMAC_obj = HMAC(K, hashlib.sha256)
        hmac = HMAC_obj.compute(salt.encode())
        
        if hmac == hmac_received:
            return "OK"

class Initiate:
    
    def GET(self):
        
        global K, salt
        
        params = web.input()
        I = params.I
        A = int(params.A)
        
        b = random.randint(0, N - 1)
        B = k*v + pow(g, b, N)
        
        uH = hashlib.sha256(str(A).encode()+str(B).encode()).hexdigest()
        u = int(uH, 16)
        # S will be zero since modulo N will be zero for 0 and multiples of N
        S = pow(A * pow(v, u, N), b, N)
        K = hashlib.sha256(str(S).encode()).digest()
        
        return {"salt":salt, "B":B}

Test the web server.

response1 = app.request("/hello?name=")
print(response1.data)

response2 = app.request("/hello?name=hexterisk")
print(json.loads(response2.data.decode("utf-8").replace("'",'"')))

b"{'name': 'Hello, World!'}"
{'name': 'Hello, hexterisk!'}

The equation for the production of the server’s session key K boils down to:

S = (A.vᵘ)ᵇ mod N

K = hash(S)

If A is zero, then S, and consequently K will be zero. We therefore need not know the password. 

def implement_SRP_zero() -> bool:
    """
    Implement SRP(Secure Remote Password) for proposed "A" values.
    """
    
    # This loop goes over proposed values for "A" by the question.
    for A in [0, N, N*2]:
        a = random.randint(0, N - 1)

        response = app.request("/init?I=" + I + "&A=" + str(A))
        response_dict = json.loads(response.data.decode("utf-8").replace("'",'"'))
        salt = response_dict["salt"]
        B = int(response_dict["B"])

        uH = hashlib.sha256(str(A).encode()+str(B).encode()).hexdigest()
        u = int(uH, 16)

        xH = hashlib.sha256(salt.encode()+P.encode()).hexdigest()
        x = int(xH, 16)

        # S = modular_pow((B - k * modular_pow(g, x, N)), (a + u * x), N)
        # We put S=0 because we know it's going to be zero on the server side
        S = 0
        K = hashlib.sha256(str(S).encode()).digest()

        HMAC_obj = HMAC(K, hashlib.sha256)
        hmac = HMAC_obj.compute(salt.encode())

        response = app.request("/verify?hmac=" + hmac)
        assert response.data.decode("utf-8") == "OK"
        print("> Verification successful.")
        return True

> Verification successful.

Completed
 

Challenge 38: Offline dictionary attack on simplified SRP

Link

S **x = SHA256(salt|password)
v = g**x % n
C->S
I, A = g**a % n
S->C
salt, B = g**b % n, u = 128 bit random number
C
x = SHA256(salt|password)
S = B**(a + ux) % n
K = SHA256(S)
S
**S = (A * v ** u)b % n
K = SHA256(S)
C->S
Send HMAC-SHA256(K, salt)
S->C
Send “OK” if HMAC-SHA256(K, salt) validates
Note that in this protocol, the server’s “B” parameter doesn’t depend on the password (it’s just a Diffie Hellman public key).
Make sure the protocol works given a valid password.
Now, run the protocol as a MITM attacker: pose as the server and use arbitrary values for b, B, u, and salt.
Crack the password from A’s HMAC-SHA256(K, salt).

# Imports
import os
import web
import json
import time
import random
import hashlib

# Client and server agree on these values beforehand

# Generated using "openssl dhparam -text 1024".
N = int("008c5f8a80af99a7db03599f8dae8fb2f75b52501ef54a827b8a1a586f14dfb20d6b5e2ff878b9ad6bca0bb9"
        "18d30431fca1770760aa48be455cf5b949f3b86aa85a2573769e6c598f8d902cc1a0971a92e55b6e04c4d07e"
        "01ac1fa9bdefd1f04f95f197b000486c43917568ff58fafbffe12bde0c7e8f019fa1cb2b8e1bcb1f33", 16)
g = 2
k = 3
I = "hextersik@hexterisk.com"
P = "BackupU$r"

I used web.py to build the server.

urls = (
    '/hello', 'Hello',
    '/init', 'Initiate',
    '/verify', 'Verify'
)

app = web.application(urls, globals())

K = None
salt = str(random.randint(0, 2**32 - 1))
# since we can't save x, xH
v = pow(g, int(hashlib.sha256(salt.encode()+P.encode()).hexdigest(), 16), N)

class Hello:        
    
    def GET(self):
        params = web.input()
        name = params.name
        if not name:
            name = 'World'
            
        string = "Hello, " + name + "!"
        return {"name" : string}
    
class Verify:

    def GET(self):
        
        global K, salt
        
        params = web.input()
        hmac_received = params.hmac
        
        HMAC_obj = HMAC(K, hashlib.sha256)
        hmac = HMAC_obj.compute(salt.encode())
        
        if hmac == hmac_received:
            return "OK"

class Initiate:
    
    def GET(self):
        
        global K, salt
        
        params = web.input()
        I = params.I
        A = int(params.A)
        
        b = random.randint(0, N - 1)
        B = pow(g, b, N)
        
        u = random.getrandbits(128)
        S = pow(A * pow(v, u, N), b, N)
        K = hashlib.sha256(str(S).encode()).digest()
        
        return {"salt":salt, "B":B, "u":u}

Test the web server.

response1 = app.request("/hello?name=")
print(response1.data)

response2 = app.request("/hello?name=hexterisk")
print(json.loads(response2.data.decode("utf-8").replace("'",'"')))

b"{'name': 'Hello, World!'}"
{'name': 'Hello, hexterisk!'}

The idea is that if you’re able to get a MITM working, you can modify the parameters being exchanged. Therefore, you can use a dictionary attack to fetch a list of common passwords, use them to generate a session key K, and brute force the list of passwords in hopes of a successful verification.

def MITM_SRP() -> bool:
    """
    Implements simplified SRP and performs MITM.
    Performs an offline dictionary attack on it.
    """
    a = random.randint(0, N - 1)
    A = pow(g, a, N)
    
    response = app.request("/init?I=" + I + "&A=" + str(A))
    response_dict = json.loads(response.data.decode("utf-8").replace("'",'"'))
    salt = response_dict["salt"]
    B = int(response_dict["B"])
    u = int(response_dict["u"])
    
    # Uses a dictionary.
    data = open('dictionary.txt', 'r').read()
    passwords = data.split('\n')
    
    for password in passwords:
        xH = hashlib.sha256(salt.encode()+password.encode()).hexdigest()
        x = int(xH, 16)

        S = pow(B, (a + u * x), N)
        K = hashlib.sha256(str(S).encode()).digest()

        HMAC_obj = HMAC(K, hashlib.sha256)
        hmac = HMAC_obj.compute(salt.encode())

        response = app.request("/verify?hmac=" + hmac)
        
        if response.data.decode("utf-8") == "OK":
            print("> Brute force successful.")
            print("> Password found to be:", P)
            return True
            break

> Brute force successful.
> Password found to be: BackupU$r

Completed
 

Challenge 39: Implement RSA

Link

There are two annoying things about implementing RSA. Both of them involve key generation; the actual encryption/decryption in RSA is trivial.
First, you need to generate random primes. You can’t just agree on a prime ahead of time, like you do in DH. You can write this algorithm yourself, but I just cheat and use OpenSSL’s BN library to do the work.
The second is that you need an “invmod” operation (the multiplicative inverse), which is not an operation that is wired into your language. The algorithm is just a couple lines, but I always lose an hour getting it to work.
I recommend you not bother with primegen, but do take the time to get your own EGCD and invmod algorithm working.
Now:

  1. Generate 2 random primes. We’ll use small numbers to start, so you can just pick them out of a prime table. Call them “p” and “q”.
  2. Let n be p * q. Your RSA math is modulo n.
  3. Let et be (p-1)*(q-1) (the “totient”). You need this value only for keygen.
  4. Let e be 3.
  5. Compute d = invmod(e, et). invmod(17, 3120) is 2753.
  6. Your public key is [e, n]. Your private key is [d, n].
  7. To encrypt: c = me%n. To decrypt: m = cd%n
  8. Test this out with a number, like “42”.
  9. Repeat with bignum primes (keep e=3).

Finally, to encrypt a string, do something cheesy, like convert the string to hex and put “0x” on the front of it to turn it into a number. The math cares not how stupidly you feed it strings.

# Imports
import math
import random
from Crypto.Util.number import getPrime

I used Extended Euclidean Algorithm to calculate the modular inverse.

def mod_inverse(a: int, n: int) -> int: 
    """
    Computes the multiplicative inverse of a modulo n using the extended Euclidean algorithm.
    """
    
    t, r = 0, n
    new_t, new_r = 1, a

    while new_r != 0:
        quotient = r // new_r
        t, new_t = new_t, t - quotient * new_t
        r, new_r = new_r, r - quotient * new_r

    if r > 1:
        raise Exception("a is not invertible")
    if t < 0:
        t = t + n

    return t

RSA (Rivest–Shamir–Adleman) is based on the difficulty of factoring large numbers. It uses two large primes p and q, used to calculate the following parameters:

  • _n = p * q _
  • ϕ(n) = (p - 1) * (q - 1), called totient.
  • e is a value co-prime to n.
  • d = 1 mod ϕ(n)

The public key is the pair (e, n) and the private key is the pair (d, n).

For a message M, convert it into integral form m. Then:

  • Encryption: c = mᵉ mod n
  • Decryption: m = cᵈ mod n
class RSA:
    """
    Implementation of the RSA (Rivest–Shamir–Adleman) algorithm.
    """
    
    def __init__(self: object, keysize: int):
        e = 3
        et = 0
        n = 0

        while math.gcd(e, et) != 1:
            p, q = getPrime(keysize // 2), getPrime(keysize // 2)
            et = ((p - 1) * (q - 1)) // math.gcd(p - 1, q - 1)
            n = p * q

        d = mod_inverse(e, et)
        
        self.pub = (e, n)
        self.pvt = (d, n)

    def encrypt(self: object, message: bytes, byteorder="big") -> int:
        (e, n) = self.pub
        data = int.from_bytes(message, byteorder)
        
        if data < 0 or data >= n:
            raise ValueError(str(data) + ' out of range')
            
        return pow(data, e, n)
    
    def encryptnum(self: object, m: int) -> int:
        (e, n) = self.pub
        if m < 0 or m >= n:
            raise ValueError(str(m) + ' out of range')
        return pow(m, e, n)
    
    def decrypt(self: object, ciphertext: bytes, byteorder="big") -> bytes:
        (d, n) = self.pvt
        
        if ciphertext < 0 or ciphertext >= n:
            raise ValueError(str(ciphertext) + ' out of range')
        
        numeric_plain = pow(ciphertext, d, n)
        return numeric_plain.to_bytes((numeric_plain.bit_length() + 7) // 8, byteorder)
    
    def decryptnum(self: object, m: int) -> int:
        (d, n) = self.pvt
        if m < 0 or m >= n:
            raise ValueError(str(m) + ' out of range')
        return pow(m, d, n)

rsa = RSA(1024)
message = "Testing 1..2..3..."
ciphertext = rsa.encrypt(message.encode())

Completed
 

Challenge 40: Implement an E=3 RSA Broadcast attack

Link

Assume you’re a Javascript programmer. That is, you’re using a naive handrolled RSA to encrypt without padding.
Assume you can be coerced into encrypting the same plaintext three times, under three different public keys. You can; it’s happened.
Then an attacker can trivially decrypt your message, by:
Capturing any 3 of the ciphertexts and their corresponding pubkeys
Using the CRT to solve for the number represented by the three ciphertexts (which are residues mod their respective pubkeys)
Taking the cube root of the resulting number
The CRT says you can take any number and represent it as the combination of a series of residues mod a series of moduli. In the three-residue case, you have: result =
(c_0 * m_s_0 * invmod(m_s_0, n_0)) +
(c_1 * m_s_1 * invmod(m_s_1, n_1)) +
(c_2 * m_s_2 * invmod(m_s_2, n_2)) mod N_012
where:
c_0, c_1, c_2 are the three respective residues mod
n_0, n_1, n_2
m_s_n (for n in 0, 1, 2) are the product of the moduli
EXCEPT n_n — ie, m_s_1 is n_0 * n_2
N_012 is the product of all three moduli
To decrypt RSA using a simple cube root, leave off the final modulus operation; just take the raw accumulated result and cube-root it.

    # Imports
    import math

def floorRoot(n: int, s: int) -> int:
    """
    Finds the specified powered root of an integer and returns the resulting float's floor value.
    """
    
    b = n.bit_length()
    p = math.ceil(b/s)
    x = 2**p
    while x > 1:
        y = (((s - 1) * x) + (n // (x**(s-1)))) // s
        if y >= x:
            return x
        x = y
    return 1

NOTE: The attack only works if the RSA public key e is very small( say, equal to 3).

The solution to this problem lies with the Chinese Remainder Theorem.

We need the same plaintext encrypted with different public keys to recover the plaintext. According to the paper, for 

C¹ = m³ mod n¹, C² = m² mod n² and C³ = m³ mod n³,

    ⇨ C’ = m³ mod n¹n²n³

Therefore, if are able to calculate C’, we can just cube root it to get the solution.

def RSA_Broadcast_Attack(message: bytes, rsa0: object, rsa1: object, rsa2: object) -> bytes:
    """
    Uses the Chinese Remainder Theorem (CRT) to break e=3 RSA given three ciphertexts of the same plaintext.
    This attack could be easily coded to work also when a different number of ciphertexts is provided.
    Check here for reference: https://crypto.stanford.edu/pbc/notes/numbertheory/crt.html
    """

    # Obtain the N from the public keys of the RSA objects.
    n0 = rsa0.pub[1]
    n1 = rsa1.pub[1]
    n2 = rsa2.pub[1]
    
    # Encrypt the integer of the message via all three RSA objects.
    plainnum = int.from_bytes(message, "big")
    c0 = rsa0.encryptnum(plainnum)
    c1 = rsa1.encryptnum(plainnum)
    c2 = rsa2.encryptnum(plainnum)
    
    # Can't do N/n0 for ms0 instead because floating point operations arent accurate
    N = n0 * n1 * n2
    ms0 = n1 * n2
    ms1 = n0 * n2
    ms2 = n0 * n1
    
    r0 = (c0 * ms0 * mod_inverse(ms0, n0))
    r1 = (c1 * ms1 * mod_inverse(ms1, n1))
    r2 = (c2 * ms2 * mod_inverse(ms2, n2))
    
    R = (r0 + r1 + r2) % N
    m = floorRoot(R, 3)
    
    return m.to_bytes((m.bit_length() + 7) // 8, "big")

message = "This is RSA Broadcast Attack"
RSA_Broadcast_Attack(message.encode(), RSA(256), RSA(256), RSA(256)).decode("utf-8")

"This is RSA Broadcast Attack"

Completed