Set 4

Refer to this repository for solution scripts and the IPython Notebook pertaining to the explanations here.

Challenge 25: Break “random access read/write” AES CTR

Back to CTR. Encrypt the recovered plaintext from this file (the ECB exercise) under CTR with a random key (for this exercise the key should be unknown to you, but hold on to it).

Now, write the code that allows you to “seek” into the ciphertext, decrypt, and re-encrypt with different plaintext. Expose this as a function, like, “edit(ciphertext, key, offset, newtext)”.

Imagine the “edit” function was exposed to attackers by means of an API call that didn’t reveal the key or the original plaintext; the attacker has the ciphertext and controls the offset and “new text”.

Recover the original plaintext.

# Imports
import os
import base64
import itertools

# Given
data = open("25.txt", "r").read()

We have already established the fact that xoring multiple strings with the same keystream is a very bad idea.

Now, the fact that CTR allows us to seek into the ciphertext, we can use it to our advantage to manipulate the ciphertext. We can encrypt our own text with the same keystream and then replace the bytes at the indices specified to be modified/overwritten.

def edit(ciphertext: bytes, key: bytes, offset: int, newtext: bytes, nonce: int) -> bytes:
    """
    Seek into the ciphertext at the given offset and edit the ciphertext to add the newtext's cipher at the offset.
    """
    keystream = b""
    # Obtain the keystream used to encrypt in the AES CTR Mode.
    # Encrypting newtext to be inserted at offset requires CTR keystream at that offset too.
    stream = CTR_keystream_generator(key, nonce)
    for i in itertools.islice(stream, offset, offset+len(newtext)):
        keystream += i.to_bytes(1, "big")
    
    # Get the cipher for newtext.
    append_cipher = xor_bytes(newtext, keystream)
    
    # Append the cipher of newtext to original cipher.
    result = ciphertext[:offset] + append_cipher
    if len(result) < len(ciphertext):
        return result + ciphertext[len(result):]
    return result

Test the edit function.

random_key = os.urandom(16)
nonce = 0

plaintext = b"hello there"
cipher = CTR(plaintext, random_key, nonce)
print("Original text:", CTR(cipher, random_key, nonce).decode("utf-8"))
edited_cipher = edit(cipher, random_key, 4, b"####", nonce)
print("Edited text:", CTR(edited_cipher, random_key, nonce).decode("utf-8"))

Original text: hello there
Edited text: hell####ere

# If you give text as \x00 it gives out keystream, xors keystream with 0 and thus can decode keystream 
# by using offset as 0.
recovered_bytes = base64.b64decode(data)

random_key = os.urandom(16)
nonce = 0

ciphertext = CTR(recovered_bytes, random_key, nonce)
recovered_keystream = edit(ciphertext, random_key, 0, b'\x00'*len(ciphertext), nonce)
deciphered_bytes = xor_bytes(ciphertext, recovered_keystream)

Completed

Challenge 26: CTR bitflipping

Link

There are people in the world that believe that CTR resists bit flipping attacks of the kind to which CBC mode is susceptible.
Re-implement the CBC bitflipping exercise from earlier to use CTR mode instead of CBC mode. Inject an “admin=true” token.

# Imports
import os

# Given
prepend_string = "comment1=cooking%20MCs;userdata="
append_string = ";comment2=%20like%20a%20pound%20of%20bacon"

Function to prepend the URL encoded string to text and encrypt it with CTR.

def encryptor(text: bytes, key: bytes, nonce: int) -> bytes:
    """
    Prepends the string to given text and encrypts with CTR.
    """
    plaintext =  (prepend_string.encode() + text + append_string.encode()).replace(b';', b'";"').replace(b'=', b'"="')
    ciphertext = CTR(plaintext, key, nonce)
    return ciphertext

Function to decrypt the cipihertext and check if “admin=true” is present.

def decryptor(byte_string: bytes, random_key: bytes, nonce: int) -> bool:
    """
    Decrypts the ciphertext via AES CTR Mode and checks if admin is set to true.
    """
    decrypted_string = CTR(byte_string, random_key, nonce)
    if b';admin=true;' in decrypted_string:
        return True
    else:
        return False

We find out the common prefix length so as to get the length of the prepended string. We then seek to the index where our inserted text starts, we flip the bits through the xor operation and modify the ciphertext so that when it is decrypted, it reads “admin=true” somewhere in it.

target_bytes = b";admin=true;"
random_key = os.urandom(16)
nonce = 0

modified_string = b""

# we take out prefix length and then combine the recovered
# keystream from that offset onwards with inut text to produce
# the required string
prefix_length = len(os.path.commonprefix([encryptor(b'AAAA', random_key, nonce), encryptor(b'', random_key, nonce)]))
print("Prefix length: ", prefix_length)

dummy_input = b"heytheremama"
ciphertext = encryptor(dummy_input, random_key, nonce)
null_cipher = encryptor(b'\x00'*len(ciphertext), random_key, nonce)
recovered_keystream = null_cipher[prefix_length:len(ciphertext)]

injected_bytes = b""
for i in range(len(target_bytes)):
    injected_bytes += (target_bytes[i] ^ recovered_keystream[i]).to_bytes(1, "big")

modified_ciphertext = ciphertext[:prefix_length] + injected_bytes + ciphertext[prefix_length + len(injected_bytes):]

Prefix length: 38

Completed

Challenge 27: Recover the key from CBC with IV=Key

Link

Take your code from the CBC exercise and modify it so that it repurposes the key for CBC encryption as the IV.
Applications sometimes use the key as an IV on the auspices that both the sender and the receiver have to know the key already, and can save some space by using it as both a key and an IV.
Using the key as an IV is insecure; an attacker that can modify ciphertext in flight can get the receiver to decrypt a value that will reveal the key.
The CBC code from exercise 16 encrypts a URL string. Verify each byte of the plaintext for ASCII compliance (ie, look for high-ASCII values). Noncompliant messages should raise an exception or return an error that includes the decrypted plaintext (this happens all the time in real systems, for what it’s worth).
Use your code to encrypt a message that is at least 3 blocks long:
AES-CBC(P_1, P_2, P_3) -> C_1, C_2, C_3
Modify the message (you are now the attacker):
C_1, C_2, C_3 -> C_1, 0, C_1
Decrypt the message (you are now the receiver) and raise the appropriate error if high-ASCII is found.
As the attacker, recovering the plaintext from the error, extract the key:
P’_1 XOR P’_3

# Imports
import os

# Given
prepend_string = "comment1=cooking%20MCs;userdata="
append_string = ";comment2=%20like%20a%20pound%20of%20bacon"

def check_ascii_compliance(plaintext: bytes) -> bool:
    """
    Returns true if all the characters of plaintext are ASCII compliant (ie are in the ASCII table).
    """
    return all(c < 128 for c in plaintext)

NOTE: The specifications of this function are to be paid attention to. The attack is only possible if the oracle gives a feedback on the decrypted bytes being ASCII compliant, as well as returning the decrypted bytes if they aren’t.

def encryptor(text: bytes, IV: bytes, key: bytes) -> bytes:
    """
    Encrypts the text with AES CBC Mode.
    """
    plaintext = text.replace(b';', b'";"').replace(b'=', b'"="')
    ciphertext = AES_CBC_encrypt(PKCS7_pad(plaintext, len(key)), IV, key)
    return ciphertext

def decryptor(byte_string: bytes, IV: bytes, key: bytes) -> bool:
    """
    Decrypts the ciphertext via AES CBC Mode and checks if all characters are ASCII.
    """
    decrypted_string = AES_CBC_decrypt(byte_string, IV, key)
    print(len(decrypted_string), decrypted_string)
    if not check_ascii_compliance(decrypted_string):
        raise Exception(decrypted_string)

Given K(key) = IV, and that we’re in control of the cipher blocks being sent for decryption,

⇨ P¹ = Decrypt(C¹) ⊕ K

Here, since we know the plaintext and the ciphertext, if we get the intermediate state of decryption of C¹ block (ie Decrypt(C¹)), we can xor it with P¹ to get the K.

Now, feeding C¹ as the (i-1)th block for decryption to a random block Cⁱ, we get:

⇨ Pⁱ⁺¹ = Decrypt(C¹) ⊕ Cⁱ

If Cⁱ = 0,

⇨ Pⁱ⁺¹ = Decrypt(C¹), which would give us the intermediate state of decryption of C¹ block (ie Decrypt(C¹)).

Therefore, the attack is crafted as follows:

Pick a ciphertext block to focus on. Call it C¹ for simplicity.
Send C¹ || 0 || C1 to the decryption oracle.
Compute the key as K = P¹ ⊕ C¹.

Now, since the oracle checks the output for ASCII compliance, and in fact does send us the supposedly decrypted bytes when it’s non-ASCII compliant, we can thus receive the key as it gets decrypted. If the decrypted bytes happens to pass the ASCII check, pick a different cipher block to begin with.

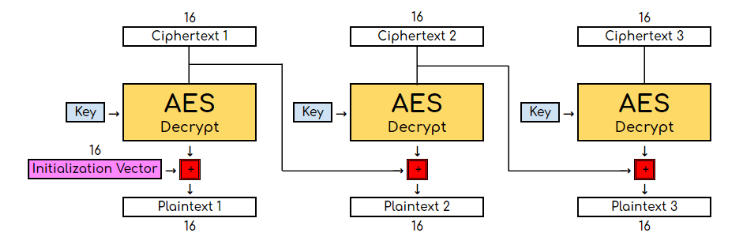AES CBC Decryption (3 blocks).

keysize = 16
random_key = os.urandom(keysize)
IV = random_key

plaintext = b"lorem=ipsum;test=fun;padding=dull"
ciphertext = encryptor(plaintext, IV, random_key)
c1 = ciphertext[:keysize]
c2 = ciphertext[keysize:2*keysize]
c3 = ciphertext[2*keysize:]

try:
    decryptor(c1 + b'\x00'*16 + c1, IV, random_key)
except Exception as e:
    decrypted_string = str(e).encode()
    p1 = decrypted_string[:keysize]
    p3 = decrypted_string[2*keysize:]
    decrypted_key = xor_bytes(p1, p3)
    print("> Key found to be:", decrypted_key)

57 b'lorem"="ipsum";"W\xc3\x9b\xc3\xb8]\xc3\x95;l=|}W`VK\xc2\xb1(;h\xc2\x86\x06uL\xc3\xacV\xc3\x87\xc2\x97~:4\xc3\x88\x00l'
> Key found to be: b'\x1aET2.\x1d\x0e\x11aZPEH\x19P^'

Completed

Challenge 28: Implement a SHA-1 keyed MAC

Link

Find a SHA-1 implementation in the language you code in.
Write a function to authenticate a message under a secret key by using a secret-prefix MAC, which is simply:
SHA1(key || message)
Verify that you cannot tamper with the message without breaking the MAC you’ve produced, and that you can’t produce a new MAC without knowing the secret key.

# Imports
import os
import struct
import hashlib

MAC (Message Authentication Code) works towards an integrity/authenticity check for a message. It can be computed on the sender’s side, and sent with the message. The receiver, on reception of the message, can compute it and verify it with the MAC received to verify that the message is authentic, and hasn’t been tampered with.

The implementation of the function is as follows:

SHA-1 works on 512 bit blocks. For a given input message m, it first appends some bits (at least 65, at most 576) so that the total length is a multiple of 512. Let’s call p the added bits (that’s the padding). The padded message is now m||p and is processed in the form of 512-bit blocks. It uses an internal compression function (traditional name because it transforms two fixed-length inputs, the message and the key, into a fixed-length output, the MAC) and maintains a running state consisting of five 32-bit words. The compression function takes as input two values of 160 bits(the running state) and 512 bits(the padded message block), respectively, and outputs 160 bits(final MAC). The processing goes like this:

The running state is initialized to a fixed, conventional value (which is given in the SHA-1 specification).
For each input block, the compression function is evaluated, with as input the current running state, and the input block; the output of the function is the new running state.
The running state after processing the last block is the hash output.

def left_rotate(value: int, shift: int) -> int:
    """
    Returns value left-rotated by shift bits. In other words, performs a circular shift to the left.
    """
    return ((value << shift) &amp;amp;amp;amp;amp;amp; 0xffffffff) | (value >> (32 - shift))


def sha1(message: bytes, ml=None, h0=0x67452301, h1=0xEFCDAB89, h2=0x98BADCFE, h3=0x10325476, h4=0xC3D2E1F0) -> bytes:
    """
    Returns a string containing the SHA1 hash of the input message. This is a pure python 3 SHA1
    implementation, written starting from the SHA1 pseudo-code on Wikipedia.
    """
    
    # Pre-processing:
    if ml is None:
        ml = len(message) * 8

    message += b'\x80'
    while (len(message) * 8) % 512 != 448:
        message += b'\x00'

    message += struct.pack('>Q', ml)

    # Process the message in successive 512-bit chunks:
    for i in range(0, len(message), 64):

        # Break chunk into sixteen 32-bit big-endian integers w[i]
        w = [0] * 80
        for j in range(16):
            w[j] = struct.unpack('>I', message[i + j * 4:i + j * 4 + 4])[0]

        # Extend the sixteen 32-bit integers into eighty 32-bit integers:
        for j in range(16, 80):
            w[j] = left_rotate(w[j - 3] ^ w[j - 8] ^ w[j - 14] ^ w[j - 16], 1)

        # Initialize hash value for this chunk:
        a = h0
        b = h1
        c = h2
        d = h3
        e = h4

        # Main loop
        for j in range(80):
            if j <= 19:
                f = d ^ (b &amp;amp;amp;amp;amp;amp; (c ^ d))
                k = 0x5A827999
            elif 20 <= j <= 39:
                f = b ^ c ^ d
                k = 0x6ED9EBA1
            elif 40 <= j <= 59:
                f = (b &amp;amp;amp;amp;amp;amp; c) | (d &amp;amp;amp;amp;amp;amp; (b | c))
                k = 0x8F1BBCDC
            else:
                f = b ^ c ^ d
                k = 0xCA62C1D6

            temp = left_rotate(a, 5) + f + e + k + w[j] &amp;amp;amp;amp;amp;amp; 0xffffffff
            e = d
            d = c
            c = left_rotate(b, 30)
            b = a
            a = temp

        # Add this chunk's hash to result so far:
        h0 = (h0 + a) &amp;amp;amp;amp;amp;amp; 0xffffffff
        h1 = (h1 + b) &amp;amp;amp;amp;amp;amp; 0xffffffff
        h2 = (h2 + c) &amp;amp;amp;amp;amp;amp; 0xffffffff
        h3 = (h3 + d) &amp;amp;amp;amp;amp;amp; 0xffffffff
        h4 = (h4 + e) &amp;amp;amp;amp;amp;amp; 0xffffffff

    # Produce the final hash value (big-endian) as a 160 bit number, hex formatted:
    return "%08x%08x%08x%08x%08x" % (h0, h1, h2, h3, h4)

The function works on producing the MAC based on SHA-1.

def sha1_mac(key: bytes, message: bytes) -> bytes:
    return sha1(key + message)

keysize = 16
random_key = os.urandom(keysize)
message = "This is a message to test that our implementation of the SHA1 MAC works properly."

hashed = sha1_mac(random_key, message.encode())

# Verify that I implemented SHA1 correctly
h = hashlib.sha1(random_key + message.encode())

Completed

Challenge 29: Break a SHA-1 keyed MAC using length extension

Link

Secret-prefix SHA-1 MACs are trivially breakable.
The attack on secret-prefix SHA1 relies on the fact that you can take the ouput of SHA-1 and use it as a new starting point for SHA-1, thus taking an arbitrary SHA-1 hash and “feeding it more data”.
Since the key precedes the data in secret-prefix, any additional data you feed the SHA-1 hash in this fashion will appear to have been hashed with the secret key.
To carry out the attack, you’ll need to account for the fact that SHA-1 is “padded” with the bit-length of the message; your forged message will need to include that padding. We call this “glue padding”. The final message you actually forge will be:
SHA1(key || original-message || glue-padding || new-message)
(where the final padding on the whole constructed message is implied)
Note that to generate the glue padding, you’ll need to know the original bit length of the message; the message itself is known to the attacker, but the secret key isn’t, so you’ll need to guess at it.
This sounds more complicated than it is in practice.
To implement the attack, first write the function that computes the MD padding of an arbitrary message and verify that you’re generating the same padding that your SHA-1 implementation is using. This should take you 5-10 minutes.
Now, take the SHA-1 secret-prefix MAC of the message you want to forge — this is just a SHA-1 hash — and break it into 32 bit SHA-1 registers (SHA-1 calls them “a”, “b”, “c”, &c).
Modify your SHA-1 implementation so that callers can pass in new values for “a”, “b”, “c” &c (they normally start at magic numbers). With the registers “fixated”, hash the additional data you want to forge.
Using this attack, generate a secret-prefix MAC under a secret key (choose a random word from /usr/share/dict/words or something) of the string:
“comment1=cooking%20MCs;userdata=foo;comment2=%20like%20a%20pound%20of%20bacon”
Forge a variant of this message that ends with “;admin=true”.

# Imports
import os
import struct

# Given
message = "comment1=cooking%20MCs;userdata=foo;comment2=%20like%20a%20pound%20of%20bacon"
payload = b";admin=true"

# Generating a pseudo random key, to be run only once.
key = os.urandom(16)

The padding function makes sure that the message received is sent in the form of a padded message. Since the last 64 bits of the block are reserved for the length of the message, the message is made sure to be (padded) upto 448 bits.

def md_pad(message: bytes) -> bytes:
    """
    Pads the message in accordance with SHA1 padding.
    """
    ml = len(message) * 8
    message += b'\x80'
    while (len(message) * 8) % 512 != 448:
        message += b'\x00'

    message += struct.pack('>Q', ml)
    return message
    
def validate(modified_message: bytes, new_md: bytes) -> bool:
    """
    Verifies the MAC.
    """
    if sha1_mac(key, modified_message) == new_md:
        return True
    return False

From the implementation, we know that the value returned from SHA1 is (H0 « 128) | (H1 « 96) | (H2 « 64) | (H3 « 32) | H4.

The output can therefore be dissolved back into H0, H1, H2, H3, and H4. These values are then used to instantiate a new SHA-1 oracle, and this new oracle can resume computation from this point on.

Now, when we get the hash h for a message m, we can compute the padding p applied to it. Let’s assume that we know m and we want to compute has for a message m’. A padding p’ will be in order. The final message comes out to be m||p||m’||p’. Since m||p is already 512 bits, m’||p’ will be computed in it’s own block. But wait, what if we already have the intermediary state between the blocks of m||p and m’||p’ ? We could just resume the computation of m’||p’ and just ignore the m||p. Well we do have the intermediary state. It’s the hash of m||p. Therefore, we could just use the hash of any random message, and use it’s value to sign any message we want to, and it would have a valid MAC. The implications of this are major. It makes forgery really easy and straight forward.

def sha1_length_extension_attack(message: bytes, original_md: bytes, payload: bytes) -> (bytes, bytes):
    """
    Perform the SHA1 length extension attack.
    """
    for key_length in range(20):
        h = struct.unpack('>5I', bytes.fromhex(original_md))
        modified_message = md_pad(b'A'*key_length + message)[key_length:] + payload
        new_md = sha1(payload, (len(modified_message) + key_length)*8, h[0], h[1], h[2], h[3], h[4])
        if validate(modified_message, new_md):
            print("> Length extension attack successful.")
            return modified_message, new_md
            break

original_md = sha1_mac(key, message.encode())
modified_message, new_md = sha1_length_extension_attack(message.encode(), original_md, payload)

> Length extension attack successful.

Completed

Challenge 30: Break an MD4 keyed MAC using length extension

Link

Second verse, same as the first, but use MD4 instead of SHA-1. Having done this attack once against SHA-1, the MD4 variant should take much less time; mostly just the time you’ll spend Googling for an implementation of MD4.

# Imports
import os
import struct
import binascii

# Given
message = "comment1=cooking%20MCs;userdata=foo;comment2=%20like%20a%20pound%20of%20bacon"
payload = b";admin=true"

# Generating a pseudo random key, to be run only once.
key = os.urandom(16)

There are four internal state variables - A, B, C, D, each 32 bits. These are initialized to:

word A: 01 23 45 67
word B: 89 ab cd ef
word C: fe dc ba 98
word D: 76 54 32 10

We also use a table of 64 values generated from the sine function, self.k.

For each chunk, which is 512 bits, we unpack into 16 words of 32-bits.

Then, we do 64 transforms, split into four rounds. each transform taking: an incrementing-by-one index into the sin table, a function f specific to the round, a lrot value, and an index into our array of 16 words.

At the end of each transform, the values are updated as follows:

a, b, c, d = d, x & 0xffffffff_, b, c_

where x is the result of the transform.

The message digest produced as output is the concat of A, B, C, D, and it is 128 bits, or 16-bytes in length.

class MD4:
    """
    This implementation resembles the one of the Wikipedia pseudo-code.
    """
    
    buf = [0x00] * 64

    _F = lambda self, x, y, z: ((x &amp;amp;amp;amp;amp;amp; y) | (~x &amp;amp;amp;amp;amp;amp; z))
    _G = lambda self, x, y, z: ((x &amp;amp;amp;amp;amp;amp; y) | (x &amp;amp;amp;amp;amp;amp; z) | (y &amp;amp;amp;amp;amp;amp; z))
    _H = lambda self, x, y, z: (x ^ y ^ z)

    def __init__(self: object, message: bytes, ml=None, A=0x67452301, B=0xefcdab89, C=0x98badcfe, D=0x10325476):
        self.A, self.B, self.C, self.D = A, B, C, D

        if ml is None:
            ml = len(message) * 8
        length = struct.pack('<Q', ml)

        while len(message) > 64:
            self._handle(message[:64])
            message = message[64:]

        message += b'\x80'
        message += bytes((56 - len(message) % 64) % 64)
        message += length

        while len(message):
            self._handle(message[:64])
            message = message[64:]

    def _handle(self: object, chunk: bytes):
        X = list(struct.unpack('<' + 'I' * 16, chunk))
        A, B, C, D = self.A, self.B, self.C, self.D

        for i in range(16):
            k = i
            if i % 4 == 0:
                A = left_rotate((A + self._F(B, C, D) + X[k]) &amp;amp;amp;amp;amp;amp; 0xffffffff, 3)
            elif i % 4 == 1:
                D = left_rotate((D + self._F(A, B, C) + X[k]) &amp;amp;amp;amp;amp;amp; 0xffffffff, 7)
            elif i % 4 == 2:
                C = left_rotate((C + self._F(D, A, B) + X[k]) &amp;amp;amp;amp;amp;amp; 0xffffffff, 11)
            elif i % 4 == 3:
                B = left_rotate((B + self._F(C, D, A) + X[k]) &amp;amp;amp;amp;amp;amp; 0xffffffff, 19)

        for i in range(16):
            k = (i // 4) + (i % 4) * 4
            if i % 4 == 0:
                A = left_rotate((A + self._G(B, C, D) + X[k] + 0x5a827999) &amp;amp;amp;amp;amp;amp; 0xffffffff, 3)
            elif i % 4 == 1:
                D = left_rotate((D + self._G(A, B, C) + X[k] + 0x5a827999) &amp;amp;amp;amp;amp;amp; 0xffffffff, 5)
            elif i % 4 == 2:
                C = left_rotate((C + self._G(D, A, B) + X[k] + 0x5a827999) &amp;amp;amp;amp;amp;amp; 0xffffffff, 9)
            elif i % 4 == 3:
                B = left_rotate((B + self._G(C, D, A) + X[k] + 0x5a827999) &amp;amp;amp;amp;amp;amp; 0xffffffff, 13)

        order = [0, 8, 4, 12, 2, 10, 6, 14, 1, 9, 5, 13, 3, 11, 7, 15]
        for i in range(16):
            k = order[i]
            if i % 4 == 0:
                A = left_rotate((A + self._H(B, C, D) + X[k] + 0x6ed9eba1) &amp;amp;amp;amp;amp;amp; 0xffffffff, 3)
            elif i % 4 == 1:
                D = left_rotate((D + self._H(A, B, C) + X[k] + 0x6ed9eba1) &amp;amp;amp;amp;amp;amp; 0xffffffff, 9)
            elif i % 4 == 2:
                C = left_rotate((C + self._H(D, A, B) + X[k] + 0x6ed9eba1) &amp;amp;amp;amp;amp;amp; 0xffffffff, 11)
            elif i % 4 == 3:
                B = left_rotate((B + self._H(C, D, A) + X[k] + 0x6ed9eba1) &amp;amp;amp;amp;amp;amp; 0xffffffff, 15)

        self.A = (self.A + A) &amp;amp;amp;amp;amp;amp; 0xffffffff
        self.B = (self.B + B) &amp;amp;amp;amp;amp;amp; 0xffffffff
        self.C = (self.C + C) &amp;amp;amp;amp;amp;amp; 0xffffffff
        self.D = (self.D + D) &amp;amp;amp;amp;amp;amp; 0xffffffff

    def digest(self: object) -> bytes:
        return struct.pack('<4I', self.A, self.B, self.C, self.D)

    def hex_digest(self: object) -> bytes:
        return binascii.hexlify(self.digest()).decode()

The padding scheme is very similar to SHA-1 — the only difference being that the length is added on as big-endian packed instead of little-endian packed.

def md_pad(message: bytes) -> bytes:
    """
    Pads the given message the same way the pre-processing of the MD4 algorithm does.
    """
    ml = len(message) * 8

    message += b'\x80'
    message += bytes((56 - len(message) % 64) % 64)
    message += struct.pack('<Q', ml)

    return message
    
def validate(modified_message: bytes, new_md: bytes) -> bool:
    """
    Verifies if the padding is correct.
    """
    if MD4(modified_message).hex_digest() == new_md:
        return True
    return False

We follow the same approach as the previous question: initialising a new instance of the oracle with an already existing, valid state derived from a valid hash.

def md4_length_extension_attack(message: bytes, original_md: bytes, payload: bytes) -> bytes:
    """
    Performs the length extension attack on an MD4.
    """
    for key_length in range(20):
        h = struct.unpack('<4I', bytes.fromhex(original_md))
        modified_message = md_pad(b'A'*key_length + message)[key_length:] + payload
        new_md = MD4(payload, (len(modified_message) + key_length)*8, h[0], h[1], h[2], h[3]).hex_digest()
        if validate(modified_message, new_md):
            print("> Length extension attack successful.")
            return modified_message, new_md
            break

original_md = MD4(message.encode()).hex_digest()
modified_message, new_md = md4_length_extension_attack(message.encode(), original_md, payload)

> Length extension attack successful.

Completed

Challenge 31: Implement and break HMAC-SHA1 with an artificial timing leak

Link

The psuedocode on Wikipedia should be enough. HMAC is very easy.
Using the web framework of your choosing (Sinatra, web.py, whatever), write a tiny application that has a URL that takes a “file” argument and a “signature” argument, like so:
http://localhost:9000/test?file=foo&signature=46b4ec586117154dacd49d664e5d63fdc88efb51
Have the server generate an HMAC key, and then verify that the “signature” on incoming requests is valid for “file”, using the “==” operator to compare the valid MAC for a file with the “signature” parameter (in other words, verify the HMAC the way any normal programmer would verify it).
Write a function, call it “insecure_compare”, that implements the == operation by doing byte-at-a-time comparisons with early exit (ie, return false at the first non-matching byte).
In the loop for “insecure_compare”, add a 50ms sleep (sleep 50ms after each byte).
Use your “insecure_compare” function to verify the HMACs on incoming requests, and test that the whole contraption works. Return a 500 if the MAC is invalid, and a 200 if it’s OK.
Using the timing leak in this application, write a program that discovers the valid MAC for any file.

# Imports
import os
import web
import json
import time
import hashlib

# Given
delay = 0.05

HMAC (keyed-Hash Message Authentication Code or Hash-based Message Authentication Code) is a specific type of MAC devised in order to overcome the broken approach used to generate MACs. Any cryptographic hash function, such as SHA-256, may be used in the calculation of an HMAC; the resulting MAC algorithm is termed HMAC-X, where X is the hash function used (e.g. HMAC-SHA256).

HMAC uses the key to derive two internal keys - inner and outer. It makes two passes to compute the final hash. The first pass uses the inner key and the message to produce an internal state(hash), and the second pass uses this state and the outer key to produce the final hash. Thus the algorithm provides better immunity against length extension attacks.

NOTE: HMAC does not encrypt the message. It’s sole purpose is to provide an integrity check functionality. The message therefore (encrypted or not) must be sent with the HMAC hash. Parties with the secret key will hash the message again themselves, and if it is authentic, the received and computed hashes will match.

class HMAC:
    """
    Computes the HMAC for the hash function given at the time of initialisation.
    This implementation resembles the one of the Wikipedia pseudo-code.
    """
    
    def __init__(self: object, random_key: bytes, hash_func: callable):
        self.hash_func = hash_func
        self.block_size = hash_func().block_size

        if len(random_key) > self.block_size:
            self.key = hash_func(random_key).digest()
        elif len(random_key) < self.block_size:
            self.key = random_key + b'\x00' * (self.block_size-len(random_key))

    def compute(self: object, message: bytes) -> bytes:
        o_key_pad = xor_bytes(self.key, b'\x5c' * self.block_size)
        i_key_pad = xor_bytes(self.key, b'\x36' * self.block_size)
        
        inner_hash = self.hash_func(i_key_pad + message).digest()
        
        return self.hash_func(o_key_pad + inner_hash).hexdigest()

I used web.py to create the server.

urls = (
    '/hello', 'Hello',
    '/test', 'Hash'
)

app = web.application(urls, globals())

HMAC_obj = HMAC(b"YELLOW_SUBMARINE", hashlib.sha1)

class Hello:        
    
    def GET(self):
        params = web.input()
        name = params.name
        if not name:
            name = 'World'
            
        string = "Hello, " + name + "!"
        return {"name" : string}

class Hash:
    
    def _insecure_compare(self, hash1, hash2, delay):
        for b1, b2 in zip(hash1, hash2):
            if b1 != b2:
                return False
            time.sleep(delay)
        return True
    
    def GET(self):
        global HMAC_obj
        params = web.input()
        file = params.file
        signature = params.signature
        delay = params.delay
        
        hmac = HMAC_obj.compute(file.encode())
        if self._insecure_compare(hmac.encode(), signature.encode(), float(delay)):
            return web.HTTPError(200)
        else:
            return web.HTTPError(500)

Test the web server.

response1 = app.request("/hello?name=")
print(response1.data)

response2 = app.request("/hello?name=hexterisk")
print(json.loads(response2.data.decode("utf-8").replace("'",'"')))

b"{'name': 'Hello, World!'}"
{'name': 'Hello, hexterisk!'}

filename = "foo"
signature = "274b7c4d98605fcf739a0bf9237551623f415fb8"
response = app.request("/test?delay=" + str(delay) + "&amp;amp;amp;amp;amp;amp;file=" + filename + "&amp;amp;amp;amp;amp;amp;signature=" + signature)
print(response)

signature = "8c80a95a8e72b3e822a13924553351a433e267d8"
response = app.request("/test?delay=" + str(delay) + "&amp;amp;amp;amp;amp;amp;file=" + filename + "&amp;amp;amp;amp;amp;amp;signature=" + signature)
print(response)

<Storage {'status': 500, 'headers': {}, 'header_items': [], 'data': b'500'}>
<Storage {'status': 200, 'headers': {}, 'header_items': [], 'data': b'200'}>

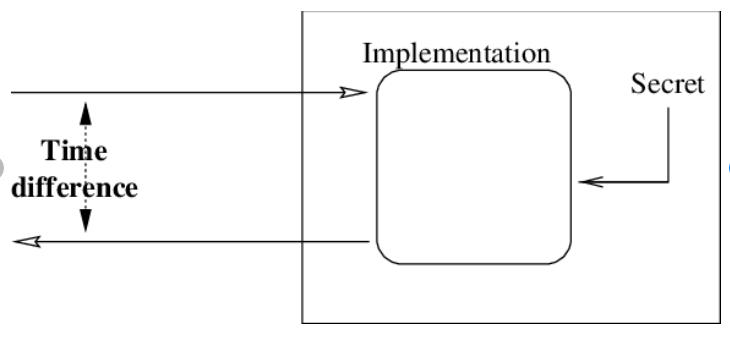Classical timing attack.

It’s a classical timing attack. We brute force all the bytes of the hash by judging the response time. Every byte check causes some delay. If for some byte the response comes back with a little more delay than all others, then it’s clear that this byte triggered the byte check for the next byte, and thus this byte was guessed correctly. Slowly the whole signature is built this way.

The function produces a 160-bit (20-byte) hash value known as a message digest, typically rendered as a hexadecimal number, 40 digits long.

signature = ""
# We go for twice the size because hexadecimal byte is 2 digits long.
for _ in range(hashlib.sha1().digest_size * 2):
    
    times = []
    # This loop goes over all 16 hexadecimal bytes.
    for i in range(16):
        start = time.time()
        response = app.request("/test?delay=" + str(delay) + "&amp;amp;amp;amp;amp;amp;file=" + filename + "&amp;amp;amp;amp;amp;amp;signature=" + signature + hex(i)[-1])
        finish = time.time()
        times.append(finish - start)
    signature += hex(times.index(max(times)))[-1]
    print("> Discovered signature:", signature)    
    response = app.request("/test?delay=" + str(delay) + "&amp;amp;amp;amp;amp;amp;file=" + filename + "&amp;amp;amp;amp;amp;amp;signature=" + signature + hex(i)[-1])
    if response.status == 200:
        print("> Brute force successful.\n> Signature:", signature)
    else:
        print("Brute force failed.")

> Discovered signature: 8
> Discovered signature: 8c
> Discovered signature: 8c8
> Discovered signature: 8c80
> Discovered signature: 8c80a
> Discovered signature: 8c80a9
> Discovered signature: 8c80a95
> Discovered signature: 8c80a95a
> Discovered signature: 8c80a95a8
> Discovered signature: 8c80a95a8e
> Discovered signature: 8c80a95a8e7
> Discovered signature: 8c80a95a8e72
> Discovered signature: 8c80a95a8e72b
> Discovered signature: 8c80a95a8e72b3
> Discovered signature: 8c80a95a8e72b3e
> Discovered signature: 8c80a95a8e72b3e8
> Discovered signature: 8c80a95a8e72b3e82
> Discovered signature: 8c80a95a8e72b3e822
> Discovered signature: 8c80a95a8e72b3e822a
> Discovered signature: 8c80a95a8e72b3e822a1
> Discovered signature: 8c80a95a8e72b3e822a13
> Discovered signature: 8c80a95a8e72b3e822a1392
> Discovered signature: 8c80a95a8e72b3e822a13924
> Discovered signature: 8c80a95a8e72b3e822a139245
> Discovered signature: 8c80a95a8e72b3e822a1392455
> Discovered signature: 8c80a95a8e72b3e822a13924553
> Discovered signature: 8c80a95a8e72b3e822a139245533
> Discovered signature: 8c80a95a8e72b3e822a1392455335
> Discovered signature: 8c80a95a8e72b3e822a13924553351
> Discovered signature: 8c80a95a8e72b3e822a13924553351a
> Discovered signature: 8c80a95a8e72b3e822a13924553351a4
> Discovered signature: 8c80a95a8e72b3e822a13924553351a43
> Discovered signature: 8c80a95a8e72b3e822a13924553351a433
> Discovered signature: 8c80a95a8e72b3e822a13924553351a433e
> Discovered signature: 8c80a95a8e72b3e822a13924553351a433e2
> Discovered signature: 8c80a95a8e72b3e822a13924553351a433e26
> Discovered signature: 8c80a95a8e72b3e822a13924553351a433e267
> Discovered signature: 8c80a95a8e72b3e822a13924553351a433e267d
> Discovered signature: 8c80a95a8e72b3e822a13924553351a433e267d8
> Brute force successful.
> Signature: 8c80a95a8e72b3e822a13924553351a433e267d8

Completed

Challenge 32: Break HMAC-SHA1 with a slightly less artificial timing leak

Link

Reduce the sleep in your “insecure_compare” until your previous solution breaks. (Try 5ms to start.) Now break it again.

    # Given
    delay = 0.005
    HMAC_obj = HMAC(b"YELLOW_SUBMARINE", hashlib.sha1)
    file = "foo"

The question is same as the previous one, the only difference being that the delay has been made smaller.

signature = ""
for _ in range(hashlib.sha1().digest_size * 2):
# We go for twice the size because hexadecimal byte is 2 digits long.
    times = []
    # This loop goes over all 16 hexadecimal bytes.
    for i in range(16):
        runtime = 0
        # Introduced more rounds so the time difference is prominent
        for _ in range(20):
            start = time.time()
            response = app.request("/test?delay=" + str(delay) + "&amp;amp;amp;amp;amp;amp;file=" + filename + "&amp;amp;amp;amp;amp;amp;signature=" + signature + hex(i)[-1])
            finish = time.time()
            runtime += finish - start
        times.append(runtime)
    signature += hex(times.index(max(times)))[-1]
    print("> Discovered signature:", signature)

response = app.request("/test?delay=" + str(delay) + "&amp;amp;amp;amp;amp;amp;file=" + filename + "&amp;amp;amp;amp;amp;amp;signature=" + signature + hex(i)[-1])
if response.status == 200:
    print("> Brute force successful.\n> Signature:", signature)
else:
    print("Brute force failed.")

Completed