Refer to this repository for solution scripts and the IPython Notebook pertaining to the explanations here.

Challenge 1: Convert hex to base64

Link

The string:
49276d206b696c6c696e6720796f757220627261696e206c696b65206120706f697 36f6e6f7573206d757368726f6f6d
Should produce:
SSdtIGtpbGxpbmcgeW91ciBicmFpbiBsaWtlIGEgcG9pc29ub3VzIG11c2hyb29t
So go ahead and make that happen.
You’ll need to use this code for the rest of the exercises.

Data, essentially raw bytes/binary (0, 1), can be represented in various forms and formats as required. These representations may be used for simply the presentation of data, or may be required by some protocol so as to prevent misinterpretation of data.

Hex

Hexadecimal is a representation format where the base for the numbers is 16. This implies that our notation consists of 16 digits (0, 1, 2, 3, 4, 5, 6, 7, 8, 9, a, b, c, d, e and f), instead of the usual 10 that we use in our base 10 system.

It is preferable over the standard binary that computers store at the low level because:

  • Readability: Hexadecimal in it’s set uses digits that overlap with the common base-10 counting system and therefore it’s easier to read and write.
  • Higher information density: Any number between 0 and 255 can be represented using 2 hex digits, while binary would require 8 digits for the same. This poses a problem as numbers start to get bigger.

Each purple tick is when a new digit is added when representing numbers.

It is preferable over the standard decimal representation that we generally use because binary and decimal never align. However, binary and hex do in fact align every 4 binary digits. This implies that a hexadecimal digit can be represented by 4 binary digits. The main reason for this is the fact that binary is a base 2 system, and therefore is compatible with any system with the specification 2ⁿ (hex is 2⁴).

Base64

An encoding scheme generally used when data needs to be transferred or stored, devised to support MIME (specifically embedding media assets inside textual assets such as HTML). Each base64 digit represents 6-bit of data, therefore a 24-bit data is represented by 4 base64 digits. Binary aligns with base64 since it is of the form 2ⁿ (base64 is 2⁶).

# Imports
from base64 import b64encode

# Given
hex_string = "49276d206b696c6c696e6720796f757220627261696e206c696b65206120706f69736f6e6f7573206d757368726f6f6d"
target_string = "SSdtIGtpbGxpbmcgeW91ciBicmFpbiBsaWtlIGEgcG9pc29ub3VzIG11c2hyb29t"

Convert given hex string to bytes.

byte_string = bytes.fromhex(hex_string)

Convert this byte string to a base64 encoded string.

base64_byte_string = b64encode(byte_string)
Completed

 

Challenge 2: Fixed XOR

Link

Write a function that takes two equal-length buffers and produces their XOR combination.
If your function works properly, then when you feed it the string:
1c0111001f010100061a024b53535009181c
… after hex decoding, and when XOR’d against:
686974207468652062756c6c277320657965
… should produce:
746865206b696420646f6e277420706c6179

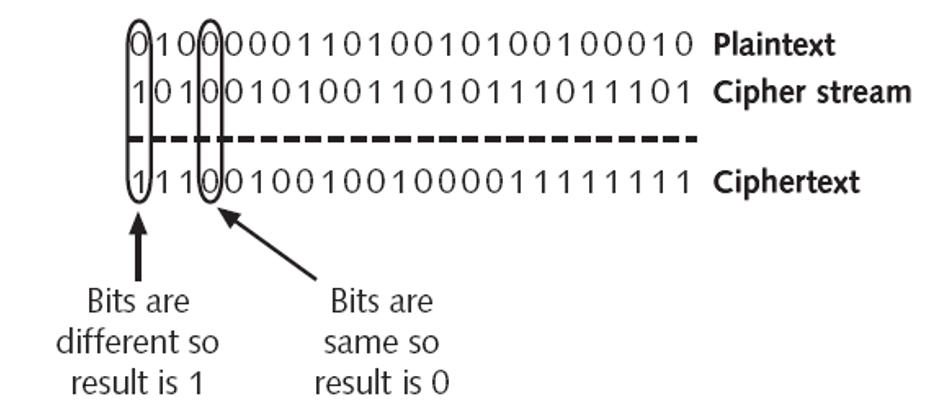The functionality is as the name suggests, ‘exclusive OR’: A ⊕ B returns true if and only if exactly one of A and B is true.

This could also be said to be telling the difference between the two:
A ⊕ B = ‘where the bits differ’. This clearly implies that A ⊕ A = 0 (byte A does not differ from itself in any bit), and,
A ⊕ 0 = A (byte A differs from 0 precisely in the bit positions that equal 1) and is also useful when thinking about toggling and encryption later on.

In cryptography, the simple XOR cipher is a type of additive cipher, an encryption algorithm that operates according to the following properties:

  • Commutative: A ⊕ B = B ⊕ A
  • Associative: A ⊕ ( B ⊕ C ) = ( A ⊕ B ) ⊕ C
  • Identity element: A ⊕ 0 = A
  • Self-inverse: A ⊕ A = 0
# Imports
from base64 import b64encode

# Given
hex_string = "1c0111001f010100061a024b53535009181c"
key_string = "686974207468652062756c6c277320657965"
target_string = "746865206b696420646f6e277420706c6179"

Function to calculate the xor of two byte strings.

def xor_bytes(enc1: bytes, enc2: bytes) -> bytes:
    """
    xor_bytes computes the xor of two byte strings and returns the final value.
    """
    cipher = b"".join([bytes(b1^b2 for b1, b2 in zip(enc1, enc2))])
    return cipher

byte_string = bytes.fromhex(hex_string)
key_byte_string = bytes.fromhex(key_string)

result = xor_bytes(byte_string, key_byte_string).hex()

Verify the solution.

assert result == target_string
Completed

 

Challenge 3: Single-byte XOR cipher

Link

The hex encoded string:
1b37373331363f78151b7f2b783431333d78397828372d363c78373e783a393b3736
… has been XOR’d against a single character. Find the key, decrypt the message.
You can do this by hand. But don’t: write code to do it for you. How? Devise some method for “scoring” a piece of English plaintext. Character frequency is a good metric. Evaluate each output and choose the one with the best score.

Monoalphabetic Cipher is a substitution cipher in which for a given key, the cipher alphabet for each plain alphabet is fixed throughout the encryption process.

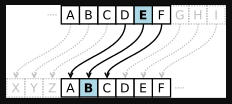Replace each plaintext letter with a different one a fixed number of places down the alphabet.

For example, if ‘A’ is encrypted as ‘D’, for any number of occurrence in that plaintext, ‘A’ will always get encrypted to ‘D’.

Single-byte Xor, as the name suggests, is when a string is xored with a single byte throughout.
It’s also known as Caesar cipher or shift cipher, it is one of the simplest and most widely known encryption techniques.
It is a type of substitution cipher in which each letter in the plaintext is replaced by a letter some fixed number of positions down the alphabet.
For example, with a left shift of 3, D would be replaced by A, E would become B, and so on.

# Imports
from itertools import zip_longest

# Given
hex_string = "1b37373331363f78151b7f2b783431333d78397828372d363c78373e783a393b3736"

Use either of the functions to brute force the single byte xor key.

def single_byte_xor_letters(ciphertext: bytes) -> dict:
    """
    Performs xor between every possible key uptil 256 and returns the key that gives the most ascii characters.
    """
    
    ascii_text_chars = list(range(97, 122)) + [32]
    best_candidate = None
    
    for i in range(2**8): # for every possible key
        
        # converting the key from a number to a byte
        candidate_key = i.to_bytes(1, "big")
        keystream = candidate_key*len(ciphertext)
        
        candidate_message = bytes([x^y for (x, y) in zip(ciphertext, keystream)])
        nb_letters = sum([ x in ascii_text_chars for x in candidate_message])
        
        # if the obtained message has more letters than any other candidate before
        if best_candidate == None or nb_letters > best_candidate["nb_letters"]:
            # store the current key and message as our best candidate so far
            best_candidate = {"message": candidate_message.decode("utf-8"), "nb_letters": nb_letters, "key": candidate_key}
    
    return best_candidate

Frequency Analysis consists of counting the occurrence of each letter in a text.
It is based on the fact that, in any given piece of text, certain letters and combinations of letters occur with varying frequencies.
For instance, given a section of English language, some letters are common, while some letters are not as frequently used.

When trying to decrypt a cipher text based on a substitution cipher, we can use a frequency analysis to help identify the most recurring letters in a cipher text and hence make hypothesis of what these letters have been encoded as.
This will help us decrypt some of the letters in the text. We can then recognise patterns/words in the partly decoded text to identify more substitutions.

Frequency distribution.

We can then use the property A ⊕ ( B ⊕ A ) = B, and xor the encrypted string with the key drawn from hypothesis (from the frequency analysis) to get the original message back.

def calculate_score(text: str) -> float:
    """
    Calculates score of the given text based on a frequency chart of english alphabets.
    """
    
    # Block for frequency analysis
    frequency_chart = {
        'E': 12.70, 'T': 9.06, 'A': 8.17, 'O': 7.51, 'I': 6.97, 'N': 6.75, 'S': 6.33, 'H': 6.09, 
        'R': 5.99, 'D': 4.25, 'L': 4.03, 'C': 2.78, 'U': 2.76, 'M': 2.41, 'W': 2.36, 'F': 2.23,
        'G': 2.02, 'Y': 1.97, 'P': 1.93, 'B': 1.29, 'V': 0.98, 'K': 0.77, 'J': 0.15,
        'X': 0.15, 'Q': 0.10, 'Z': 0.07, ' ': 35
    }
    
    score = 0.0
    for letter in text.upper():
        score += frequency_chart.get(letter, 0)
    return score

def single_byte_xor_score(ciphertext: bytes) -> dict:
    max_score = 0
    key = ''
    plaintext = ""
    
    for testkey in range(256):
        testtext = ""
        for letter in ciphertext:
            testtext += chr(letter ^ testkey)
        
        cur_score = calculate_score(testtext)
        if cur_score > max_score:
            max_score = cur_score
            key = chr(testkey)
            plaintext = testtext
            
    return {"score" : max_score, "key" : key, "message" : plaintext}

byte_string = bytes.fromhex(hex_string)

print("Using scoring technique...")
single_byte_xor_score(byte_string)['message']

Using scoring technique…
“Cooking MC’s like a pound of bacon”

print("Using ASCII counting technique...")
single_byte_xor_letters(byte_string)['message']

Using ASCII counting technique…
“Cooking MC’s like a pound of bacon”

Completed

 

Challenge 4: Detect single-character XOR

Link

One of the 60-character strings in this file has been encrypted by single-character XOR.
Find it.
(Your code from #3 should help.)

# Given
inf = open("4.txt", "r")
hex_data = inf.read()

# Creates a list of lines taken from the file.
byte_strings = []
for line in hex_data.split():
    byte_line = bytes.fromhex(line)
    byte_strings.append(byte_line)

Same as before, only difference being that a list of encrypted strings are obtained from a file, and their scores are compared amongst them too.

plaintext = ""
max_score = 0

# Runs the previous code against all lines in the file.
for line in byte_strings:
    result = single_byte_xor_score(line)
    cur_score = result["score"]
    testtext = result["message"]
    if cur_score > max_score:
        max_score = cur_score
        plaintext = testtext

plaintext

‘Now that the party is jumping\n’

Completed

 

Challenge 5: Implement repeating-key XOR

Link

Here is the opening stanza of an important work of the English language:
Burning ’em, if you ain’t quick and nimble
I go crazy when I hear a cymbal
Encrypt it, under the key ICE, using repeating-key XOR.
In repeating-key XOR, you’ll sequentially apply each byte of the key; the first byte of plaintext will be XOR’d against I, the next C, the next E, then I again for the 4th byte, and so on.
It should come out to:
0b3637272a2b2e63622c2e69692a23693a2a3c6324202d623d63343c2a26226324272765272
a282b2f20430a652e2c652a3124333a653e2b2027630c692b20283165286326302e27282f Encrypt a bunch of stuff using your repeating-key XOR function. Encrypt your mail. Encrypt your password file. Your .sig file. Get a feel for it.
I promise, we aren’t wasting your time with this.

Polyalphabetic Cipher is a substitution cipher in which the cipher alphabet for the plain alphabet may be different at different places during the encryption process.

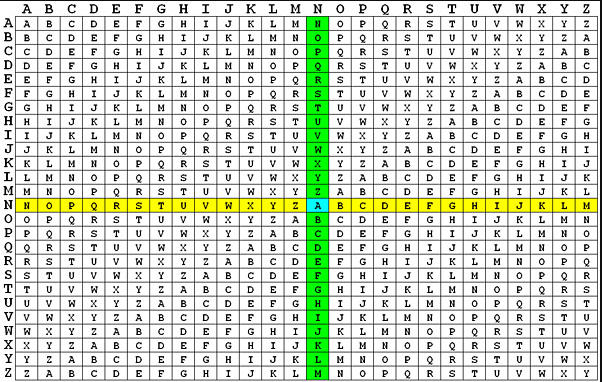Vigenère square.

Vigenère Cipher uses a Vigenère square or Vigenère table, having the alphabets written out 26 times in different rows, each alphabet shifted cyclically to the left compared to the previous alphabet, corresponding to the 26 possible Caesar ciphers.
At different points in the encryption process, the cipher uses a different alphabet from one of the rows. The alphabet used at each point depends on a repeating keyword.

Repeating XOR Cipher is where the key is shorter than the message and the key is duplicated/repeated letter-for-letter in order to cover the whole message. Then each byte of the plain text is xored with each according byte of the key. It’s a variant of Vigenère Cipher where the encryption is xor.

# Given
plaintext = "Burning 'em, if you ain't quick and nimble\nI go crazy when I hear a cymbal"
key = "ICE"
target_string = "0b3637272a2b2e63622c2e69692a23693a2a3c6324202d623d63343c2a26226324272765272a282b2f20430a652e2c652a3124333a653e2b2027630c692b20283165286326302e27282f"

def repeated_xor(text: bytes, key: bytes) -> bytes:
    """
    Performs xor between given text and key. If the length is unequal, key repeats.
    """
    quotient, remainder = divmod(len(text), len(key))
    return bytes([x ^ y for x, y in zip(text, bytes(key * quotient + key[:remainder]))])

byte_string = plaintext.encode()
bytekey = key.encode()

ciphertext = repeated_xor(byte_string, bytekey)

assert target_string == ciphertext.hex()
Completed

 

Challenge 6: Break repeating-key XOR

Link

There’s a file here. It’s been base64’d after being encrypted with repeating-key XOR.
Decrypt it.
Here’s how:

  1. Let KEYSIZE be the guessed length of the key; try values from 2 to (say) 40.
  2. Write a function to compute the edit distance/Hamming distance between two strings. The Hamming distance is just the number of differing bits. The distance between:
    this is a test
    and
    wokka wokka!!!
    is 37. Make sure your code agrees before you proceed.
  3. For each KEYSIZE, take the first KEYSIZE worth of bytes, and the second KEYSIZE worth of bytes, and find the edit distance between them.
    Normalize this result by dividing by KEYSIZE.
  4. The KEYSIZE with the smallest normalized edit distance is probably the key. You could proceed perhaps with the smallest 2-3 KEYSIZE values.
    Or take 4 KEYSIZE blocks instead of 2 and average the distances.
  5. Now that you probably know the KEYSIZE: break the ciphertext into blocks of KEYSIZE length.
  6. Now transpose the blocks: make a block that is the first byte of every block, and a block that is the second byte of every block, and so on.
  7. Solve each block as if it was single-character XOR. You already have code to do this.
  8. For each block, the single-byte XOR key that produces the best looking histogram is the repeating-key XOR key byte for that block.
    Put them together and you have the key.
    This code is going to turn out to be surprisingly useful later on. Breaking repeating-key XOR (“Vigenere”) statistically is obviously an academic exercise, a “Crypto 101” thing. But more people “know how” to break it than can actually break it, and a similar technique breaks something much more important.
# Imports
from base64 import b64decode

# Given
inf = open("6.txt", "r")
b64_data = inf.read()

byte_data = b64decode(b64_data)

def hamming_distance(text1: bytes, text2: bytes) -> int:
    """
    Calculates the Hamming Distance between the given byte strings.
    """
    
    distance = 0
    
    dec_list = [b1 ^ b2 for b1, b2 in zip(text1, text2)]
    for decimal in dec_list:
        distance += bin(decimal).count("1")
        
    if len(text1) > len(text2):
        diff = len(text1) - len(text2)
        text = text1
    else:
        diff = len(text2) - len(text1)
        text = text2
        
    for i in range(1, diff+1):
        distance += bin(text[-i]).count("1")
        
    return distance

def break_repeated_xor_keysize(ciphertext: bytes) -> int:
    """
    Approximates the keysize based on the hamming distance between different blocks of ciphertexts.
    Returns the keysize with least hamming distance between consecutive sets of ciphertext.
    """
    
    keysize = 0
    min_distance = 100000
    for key in range(2, 41):
        edit_distance = 0
        blocks = [ciphertext[i*key:(i+1)*key] for i in range(4)]
        for i in range(0, len(blocks)):
            for j in range(0, len(blocks)):
                edit_distance += hamming_distance(blocks[i], blocks[j])
        
        normalized_distance = edit_distance/key
        
        if normalized_distance < min_distance:
            min_distance = normalized_distance
            keysize = key
    
    return keysize

Creates blocks of ciphertext in preparation of brute forcing the xor keysize. When we have the key length, we can group together ciphertext bytes that share the same key byte.

keysize = break_repeated_xor_keysize(byte_data)
cipher_blocks = [byte_data[i:i+keysize] for i in range(0, len(byte_data), keysize)]

#To remove the last block with less characters.
cipher_blocks.pop()
cipher_block_size = len(cipher_blocks[0])

Brute force the key, one letter at a time.
A repeating key means that the letters at a fixed interval will be xored with the same value, that is, for a 4 byte key, a letter at every 4th position will be xored with the same letter of the key.

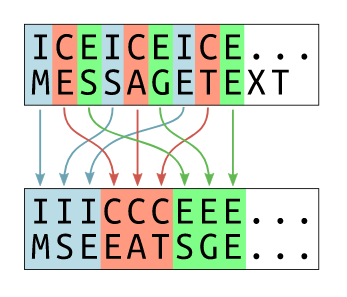Blocks of bytes at set intervals.

key = ""
for i in range(0, cipher_block_size):
    single_xor_block = b""
    
    # Construct blocks out of a fixed index from all cipher blocks.
    for block in cipher_blocks:
        single_xor_block += (block[i]).to_bytes(1, "big")
        
    # Apply frequency analysis to the block associated with this index.
    result = single_byte_xor_score(single_xor_block)
    testkey = result["key"]
    key += testkey
key

‘Terminator X: Bring the noise’

plaintext = repeated_xor(byte_data, key.encode()).decode("utf-8")
print(plaintext.strip('\n'))

I’m back and I’m ringin’ the bell A rockin’ on the mike while the fly girls yell In ecstasy in the back of me Well that’s my DJ Deshay cuttin’ all them Z’s Hittin’ hard and the girlies goin’ crazy Vanilla’s on the mike, man I’m not lazy.

I’m lettin’ my drug kick in It controls my mouth and I begin To just let it flow, let my concepts go My posse’s to the side yellin’, Go Vanilla Go!

Smooth ‘cause that’s the way I will be And if you don’t give a damn, then Why you starin’ at me So get off ‘cause I control the stage There’s no dissin’ allowed I’m in my own phase The girlies sa y they love me and that is ok And I can dance better than any kid n’ play

Stage 2 – Yea the one ya’ wanna listen to It’s off my head so let the beat play through So I can funk it up and make it sound good 1-2-3 Yo – Knock on some wood For good luck, I like my rhymes atrocious Supercalafragilisticexpialidocious I’m an effect and that you can bet I can take a fly girl and make her wet.

I’m like Samson – Samson to Delilah There’s no denyin’, You can try to hang But you’ll keep tryin’ to get my style Over and over, practice makes perfect But not if you’re a loafer.

You’ll get nowhere, no place, no time, no girls Soon – Oh my God, homebody, you probably eat Spaghetti with a spoon! Come on and say it!

VIP. Vanilla Ice yep, yep, I’m comin’ hard like a rhino Intoxicating so you stagger like a wino So punks stop trying and girl stop cryin’ Vanilla Ice is sellin’ and you people are buyin’ ‘Cause why the freaks are jockin’ like Crazy Glue Movin’ and groovin’ trying to sing along All through the ghetto groovin’ this here song Now you’re amazed by the VIP posse.

Steppin’ so hard like a German Nazi Startled by the bases hittin’ ground There’s no trippin’ on mine, I’m just gettin’ down Sparkamatic, I’m hangin’ tight like a fanatic You trapped me once and I thought that You might have it So step down and lend me your ear ‘89 in my time! You, ‘90 is my year.

You’re weakenin’ fast, YO! and I can tell it Your body’s gettin’ hot, so, so I can smell it So don’t be mad and don’t be sad ‘Cause the lyrics belong to ICE, You can call me Dad You’re pitchin’ a fit, so step back and endure Let the witch doctor, Ice, do the dance to cure So come up close and don’t be square You wanna battle me – Anytime, anywhere

You thought that I was weak, Boy, you’re dead wrong So come on, everybody and sing this song

Say – Play that funky music Say, go white boy, go white boy go play that funky music Go white boy, go white boy, go Lay down and boogie and play that funky music till you die.

Play that funky music Come on, Come on, let me hear Play that funky music white boy you say it, say it Play that funky music A little louder now Play that funky music, white boy Come on, Come on, Come on Play that funky music

test(True)
Completed

 

Challenge 7: AES in ECB mode

Link

The Base64-encoded content in this file has been encrypted via AES-128 in ECB mode under the key
“YELLOW SUBMARINE”.
(case-sensitive, without the quotes; exactly 16 characters; I like “YELLOW SUBMARINE” because it’s exactly 16 bytes long, and now you do too).
Decrypt it. You know the key, after all.
Easiest way: use OpenSSL::Cipher and give it AES-128-ECB as the cipher.

AES ECB Decryption.

AES stands for Advanced Encryption Standard.
The simplest of the encryption modes of AES is the ECB (Electronic Codebook) mode. mode. The message is divided into blocks, and each block is encrypted separately.
The blocksize(same as the keysize) can be 128, 192 or 256 bits long.

# Imports
import base64
from Crypto.Cipher import AES

# Given
inf = open("7.txt", "r")
b64_data = inf.read()

key = b"YELLOW SUBMARINE"

def AES_ECB_decrypt(ciphertext: bytes, key: bytes) -> bytes:
    """
    Decrypts a ciphertext encrypted with AES ECB Mode.
    """
    cipher = AES.new(key, AES.MODE_ECB)
    return cipher.decrypt(ciphertext)

byte_data = base64.b64decode(b64_data)
byte_text = AES_ECB_decrypt(byte_data, key)

#last 4 rubbish bytes is pkcs7 padding of \x04
byte_text

b"I’m back and I’m ringin’ the bell \nA rockin’ on the mike while the fly girls yell \nIn ecstasy in the back of me \nWell that’s my DJ Deshay cuttin’ all them Z’s \nHittin’ hard and the girlies goin’ crazy \nVanilla’s on the mike, man I’m not lazy. \n\nI’m lettin’ my drug kick in \nIt controls my mouth and I begin \nTo just let it flow, let my concepts go \nMy posse’s to the side yellin’, Go Vanilla Go! \n\nSmooth ‘cause that’s the way I will be \nAnd if you don’t give a damn, then \nWhy you starin’ at me \nSo get off ‘cause I control the stage \nThere’s no dissin’ allowed \nI’m in my own phase \nThe girlies sa y they love me and that is ok \nAnd I can dance better than any kid n’ play \n\nStage 2 – Yea the one ya’ wanna listen to \nIt’s off my head so let the beat play through \nSo I can funk it up and make it sound good \n1-2-3 Yo – Knock on some wood \nFor good luck, I like my rhymes atrocious \nSupercalafragilisticexpialidocious \nI’m an effect and that you can bet \nI can take a fly girl and make her wet. \n\nI’m like Samson – Samson to Delilah \nThere’s no denyin’, You can try to hang \nBut you’ll keep tryin’ to get my style \nOver and over, practice makes perfect \nBut not if you’re a loafer. \n\nYou’ll get nowhere, no place, no time, no girls \nSoon – Oh my God, homebody, you probably eat \nSpaghetti with a spoon! Come on and say it! \n\nVIP. Vanilla Ice yep, yep, I’m comin’ hard like a rhino \nIntoxicating so you stagger like a wino \nSo punks stop trying and girl stop cryin’ \nVanilla Ice is sellin’ and you people are buyin’ \n’Cause why the freaks are jockin’ like Crazy Glue \nMovin’ and groovin’ trying to sing along \nAll through the ghetto groovin’ this here song \nNow you’re amazed by the VIP posse. \n\nSteppin’ so hard like a German Nazi \nStartled by the bases hittin’ ground \nThere’s no trippin’ on mine, I’m just gettin’ down \nSparkamatic, I’m hangin’ tight like a fanatic \nYou trapped me once and I thought that \nYou might have it \nSo step down and lend me your ear \n'89 in my time! You, ‘90 is my year. \n\nYou’re weakenin’ fast, YO! and I can tell it \nYour body’s gettin’ hot, so, so I can smell it \nSo don’t be mad and don’t be sad \n’Cause the lyrics belong to ICE, You can call me Dad \nYou’re pitchin’ a fit, so step back and endure \nLet the witch doctor, Ice, do the dance to cure \nSo come up close and don’t be square \nYou wanna battle me – Anytime, anywhere \n\nYou thought that I was weak, Boy, you’re dead wrong \nSo come on, everybody and sing this song \n\nSay – Play that funky music Say, go white boy, go white boy go \nplay that funky music Go white boy, go white boy, go \nLay down and boogie and play that funky music till you die. \n\nPlay that funky music Come on, Come on, let me hear \nPlay that funky music white boy you say it, say it \nPlay that funky music A little louder now \nPlay that funky music, white boy Come on, Come on, Come on \nPlay that funky music \n\x04\x04\x04\x04"

Completed

 

Challenge 8: Detect AES in ECB mode

Link

In this file are a bunch of hex-encoded ciphertexts.
One of them has been encrypted with ECB.
Detect it.
Remember that the problem with ECB is that it is stateless and deterministic; the same 16 byte plaintext block will always produce the same 16 byte ciphertext.

Lack of diffusion: structure can still be made out after encryption.

Detection can be done by taking advantage of a disadvantage of this method.
The disadvantage is the lack of diffusion. Because ECB encrypts identical plaintext blocks into identical ciphertext blocks, it does not hide data patterns well.

# Imports
from base64 import b64decode
from Crypto.Cipher import AES

# Given
inf = open("8.txt", "r")
data = inf.read()

def detect_AES_ECB(ciphertext: bytes) -> int:
    """
    Detect if the AES ECB encryption mode was used for creating the given ciphertexts.
    Returns the maximum number of repititions occuring for any particular block.
    """
    blocks = [ciphertext[i:i+AES.block_size] for i in range(0, len(ciphertext), AES.block_size)]
    return len(blocks)-len(set(blocks))

Create a list of ciphertexts obtained from the file in byte format.

hex_data = data.split('\n')
ciphertext_list = [bytes.fromhex(line.strip()) for line in hex_data]

Iterate over all the ciphertexts to find out the ciphertext with maximum repititions of a block.

max_score = 0
text_ECB = ""

for cipher in ciphertext_list:
    score = detect_AES_ECB(cipher)
    if score > max_score:
        max_score = score
        text_ECB = cipher
        
print("Number of repitions: {}".format(max_score))
print("ECB ciphered text index: {0}/{1}".format(ciphertext_list.index(text_ECB), len(ciphertext_list)))

Number of repitions: 3 ECB ciphered text index: 132/205

Completed